Jump to content
  • entries
    30
  • comments
    6
  • views
    7,289

Standard Deviation

evan

Entry posted by evan

721 views

 Share

While we use percent error to dictate how far we off in class, there are far more efficient ways of defining the error of the set. Standard deviation, for example, given a value, will give rise to numbers that fall within one S.D., two S.D. and so on.

"One can find the standard deviation of an entire population in cases (such as standardized testing) where every member of a population is sampled. In cases where that cannot be done, the standard deviation σ is estimated by examining a random sample taken from the population. An estimator for σ used when sample size is very large is the standard deviation of the sample, denoted by sN and defined as follows:"

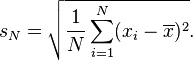
6f360d532d8c7d6fee92da6f11a96f8a.png

This method is effective for creating intervals for which certain points would have to lie within and give us the ability to decide on percent error for an entire group of values. The closer the value of S.D. approaches 0, the less the error percent is.

 Share

0 Comments

Recommended Comments

There are no comments to display.

Guest
Add a comment...

×   Pasted as rich text.   Paste as plain text instead

  Only 75 emoji are allowed.

×   Your link has been automatically embedded.   Display as a link instead

×   Your previous content has been restored.   Clear editor

×   You cannot paste images directly. Upload or insert images from URL.

×

Terms of Use

The pages of APlusPhysics.com, Physics in Action podcasts, and other online media at this site are made available as a service to physics students, instructors, and others. Their use is encouraged and is free of charge. Teachers who wish to use materials either in a classroom demonstration format or as part of an interactive activity/lesson are granted permission (and encouraged) to do so. Linking to information on this site is allowed and encouraged, but content from APlusPhysics may not be made available elsewhere on the Internet without the author's written permission.

Copyright Notice

APlusPhysics.com, Silly Beagle Productions and Physics In Action materials are copyright protected and the author restricts their use to online usage through a live internet connection. Any downloading of files to other storage devices (hard drives, web servers, school servers, CDs, etc.) with the exception of Physics In Action podcast episodes is prohibited. The use of images, text and animations in other projects (including non-profit endeavors) is also prohibited. Requests for permission to use such material on other projects may be submitted in writing to info@aplusphysics.com. Licensing of the content of APlusPhysics.com for other uses may be considered in the future.

APlusPhysics Books

APlusPhysics Books

×
×
  • Create New...