I made a post a while back about the physics behind pinch harmonics - but, since there is a multitude of other guitar techniques, there's a lot more physics to be explored with this instrument.

Think about your all-time favorite guitar solo, and I'll guarantee you that there is bending somewhere in it. It's the technique that must be mastered to make a decent solo, and it's in all of the best ones: it's ever-present in legendary solos such as Pink Floyd's "Comfortably Numb", Lynyrd Skynyrd's "Freebird", and Eagles' "Hotel California", just to scratch the surface.

Surprisingly, there's a whole bunch of complicated equations to describe the nature of bending, relating the bend angle theta to a change in frequency. An impressive and detailed paper was written about all of these techniques by David Robert Grimes, an Oxford scientist who obviously has a passion for this stuff. I'll be referencing his findings throughout these posts.

First of all, the fundamental frequency for a bent string can be described by 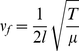where l is string length, T is its tension, and u is its linear mass density. With the application of an extending force, its bend frequency can be given in terms of the bend angle. 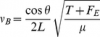Theta is the bend angle, and F subscript E is the perpendicular force exerted on the fretboard. Note that this equation only holds up when assuming that the increase in string length caused by bending is negligible.

But as we have learned, the magnitude of the restoring force of an elastic object is given by F = kx, Hooke's Law, where k is the elastic constant and x is the displacement. This can be rearranged using Young's modulus (E), which depends on material, and the string's cross-sectional area (A). kx and EA both represent the stiffness of the string. Therefore, we can replace F subscript E with known variables, and with some simplification, end up with an equation for the frequency of the bent string: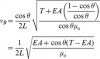

Some side notes are that 1. Young's Modulus, a measurement of stiffness, vary due to string material. 2. The area also varies from string to string - some guitarists prefer thicker strings than others. 3. According to Grimes, the typical bend angle does not exceed 1.5 degrees.

Next time, we'll look at vibrato, which, excitingly enough, involves derivatives. Woohoo.

Citation:

Grimes, David R. "String Theory - The Physics of String-Bending and Other Electric Guitar Techniques." PLOS ONE:. N.p., 23 July 2014. Web. 23 Nov. 2014.