Doctor Who Season 3 Episode 9: "Human Nature"
I like this episode because it has a really cool example of projectile motion. (Read the next line BEFORE you play the video please or you might be a bit confused).
Skip to around 1:15 in this video and watch (this is the only video I could find it in) and you'll see. The Doctor (or John Smith in this one, he has forgotten who he actually in this episode) manages to throw a cricket ball in the exact way that it hits a stack of poles that fall over and cause a brick to launch and hit a metal jug that stops the women from push her baby- inadvertently- under the falling piano.

Yeah ok, so it is a little far-fetched but physically it is possible. I do not know any exact distances or times but with the help of 1-D Kinematic equations we could calculate the exact velocity and angle at which the Doctor had to throw the object for it to the poles the way that it did. One could also calculate exactly what angle the brick flew from when it left the wooden plank that caused it to hit the metal jug. You only need these four equations.
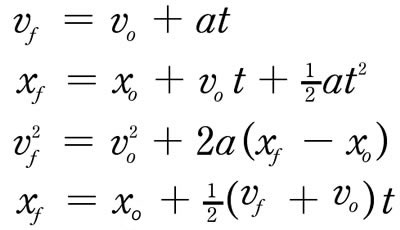
(Where Vo= intial velocity, Vf= final velocity, a= acceleration, t= time, Xo= intial x-position and Xf= final x-position)
Normally I used X= Xf - Xo instead but these equations work just fine. When a projectile is fired at an angle, as it is in this case, the velocity is split into vector components. Then there is essentially two problems, the motion in the X-plane (horizontal) and the motion in the Y-plane (vertical). The one measurement that remains constant in both is the time it takes for the projectile to land. There really is not enough information here for me to able to calculate anything but the first I would do is figure out the angle and the initial speed (it would have to be measured somehow). If I had those values I would look at the Y-plane because if the projectile is on Earth than you ALWAYS know its acceleration in the Y-plane (g= 9.81 m/s2). I suppose I would have to time the ball in this case since I have no way- at this point- to find a final velocity. Than the first equation could help me find Vf in the Y-plane. If we assume- which is never good- that it landed at the same angle (or try to find that actual angle that it land with some how) than we could use trig find the final velocity in the X-plane. All together we initial X velocity and the measured time we could find the total x distance and the acceleration in the X-plane. That involves ALOT of assumptions in this case, but as far as this type of motion goes, this clip from Doctor Who actually does fit the bill.

Ok, that would be it for quick basic projectile motion lesson! Thanks for reading!



0 Comments
Recommended Comments
There are no comments to display.