The Leaning Tower of Lire

Recently in my BC Calc class, we've been talking about series and in some cases the application of them. The harmonic series is especially applicable to music: in music, strings of the same material, diameter, and tension whose lengths form a harmonic series produce harmonic tones. Another application of the harmonic series is the Leaning Tire of Lire, a theoretical structure. Suppose that an unlimited identical books are stacked on the edge of a table in such a way that the maximize the overhang. In order to maximize overhang but prevent the structure from collapsing, we can apply the formula for calculating center of mass: c= (x₁M₁ + x₂M₂) / (M₁+M₂). In order to maximize the overhang, we need to stack the books in a way such that their center of gravity remains at x=0. This prevents the weight of the stack from applying a torque to the stack, which would result in an angular acceleration and the toppling of our structure. If we consider the center of mass of the stack with n+1 books, we get the following: 

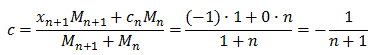
The length of the overhang, therefore, can be modeled by the harmonic series, 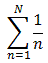. Theoretically, the harmonic series will balance with an infinite number of books. It takes 31 books for the overhang to be two books long, 227 books for the overhand to be 3 books long, and over 272 million books for the overhang to be 10 books long. Crazy stuff.