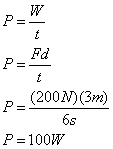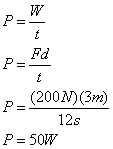Tag Archives: force
Power
Defining Power
Power is a term used quite regularly in all aspects of life. We talk about how powerful the new boat motor is, the power of positive thinking, and even the power company’s latest bill. All of these uses of the term power relate to how much work can be done in some amount of time.
In physics, work is the process of moving an object by applying a force. The rate at which the force does work is known as power (P). The units of power are the units of work divided by time, or Joules per second, known as a watt (W).
Since power is the rate at which work is done, it is possible to have the same amount of work done but with different supplied power, if the time is different.
Question: Jennifer pushes a sofa 3 meters across the floor by applying a force of 200N. If it takes her 6 seconds to push the sofa, what amount of power did she supply?
Answer:
Question: Kevin pushes the same sofa 3 meters across the floor by applying a force of 200N. Kevin, however, takes 12 seconds to push the sofa. What amount of power did Kevin supply?
Answer:
As you can see, although Jennifer and Kevin both did 600J of work in pushing the softa, Jennifer supplied twice the power of Kevin because she did the same work in half the time!
Calculating Power
There’s more to the story, however. Since power is defined as work over time, we can write the equation for power as:
And because work is equal to force (in the direction of the displacement) multiplied by displacement, we can replace work in the equation with F*d:
Looking carefully at this equation, you can observe a displacement divided by time. Since displacement divided by time is the definition of average velocity, we can replace d/t with v in the equation to obtain:
So, not only is power equal to work done divided by the time required, it’s also equal to the force applied (in the direction of the displacement) multiplied by the velocity of the object.
Question: Motor A lifts a 5000N steel crossbar upward at a constant 2 m/s. Motor B lifts a 4000N steel support upward at a constant 3 m/s. Which motor is supplying more power?
Answer: Motor B supplies more power, as shown below:

Work
Defining Work
Sometimes we work hard. Sometimes we’re slackers. But, right now, are you doing work? And what do we mean by work?
Work — the process of moving an object by applying a force
In order for a force to qualify as having done work on an object, there must be a displacement and the force must cause the displacement.
I’m sure you can think up countless examples of work being done, but a few that spring to my mind include pushing a snowblower to clear the driveway, pulling a sled up a hill with a rope, stacking boxes of books from the floor onto a shelf, and throwing a baseball from the pitcher’s mound to home plate.
Let’s try an exercise: Which of the following are examples of work being done?

- Sandy struggles to push her stalled car, but can’t make it move.
- Jeeves the butler carries a tray above his head by one arm across the room at a constant velocity.
- A missile streaks through the upper atmosphere.
Each of these examples help us better understand the definition of work. In example 1, even though Sandy pushes her car, with all her might, the car doesn’t move, therefore no work is done.
Example 2 is a very tricky situation. In this scenario, Jeeves applies a force upward with his arm, but the tray moves horizontally. From this perspective, the force of the butler’s arm isn’t causing the displacement, therefore you could say no work is done by his arm. However, Jeeves’ legs are pushing him forward, and therefore the tray moves horizontally, so you could say from this perspective he is doing work on the tray. (In actuality, the situation is even more complex than this as we pull friction and normal forces into the equation, but for the sake of clarity, let’s move on…)

In example 3, the missile’s engines are applying a force causing it to move. But what is doing the work? The hot expanding gas is pushed backward out of the missile’s engine… so, using Newton’s 3rd Law, we observe the reactionary force of the gas pushing the missile forward, causing a displacement. Therefore, the expanding exhausted gas is doing work on the missile!
Calculating Work
Mathematically, work can be expressed by the following equation:
Where W is the work done, F is the force applied, in Newtons, and d is the object’s displacement, in meters.
The units of work can be found by a unit analysis of the work formula. If work is force multiplied by distance, the units must be the units of force multiplied by the units of distance, or newtons multiplied by meters. A newton-meter is also known as a Joule (J).

It’s important to note that when using this equation, only the force applied in the direction of the object’s displacement counts! This means that if the force and displacement vectors aren’t in exactly the same direction, you need to take the component of force in the direction of the object’s displacement. To do this, line up the force and displacement vectors tail-to-tail and measure the angle between them. Since this component of force can be calculated by multiplying the force times the cosine of the angle between the force and displacement vectors, we can re-write our work equation as:
Let’s examine a few more examples:
Question: An appliance salesman pushes a refrigerator 2 meters across the floor by applying a force of 200N. Find the work done.
Answer: Since the force and displacement are in the same direction, the angle between them is 0:
.
Question: A friend’s car is stuck on the ice. You push down on the car to provide more friction for the tires (by way of increasing the normal force), allowing the car’s tires to propel it forward 5m onto less slippery ground. How much work did you do?
Answer: You applied a downward force, yet the car’s displacement was sideways. Therefore, the angle between the force and displacement vectors is 90°, so:
.
Question: You push a crate up a ramp with a force of 10N. Despite your pushing, however, the crate slides down the ramp a distance of 4m. How much work did you do?
Answer: Since the direction of the force you applied is opposite the direction of the crate’s displacement, the angle between the two vectors is 180°.
Question: How much work is done in lifting an 8-kg box from the floor to a height of 2m above the floor?
Answer: It’s easy to see the displacement is 2m, and the force must be applied in the direction of the displacement, but what is the force? To lift the box we must match and overcome the force of gravity on the box. Therefore, the force we must apply is equal to the gravitational force, or weight, of the box:

Question:Barry, John, and Sidney pull a 30-kg wagon with a force of 500N a distance of 20m. The force acts at a 30° angle to the horizontal. Calculate the work done.
Answer:
Force vs. Displacement Graphs

The area under a force vs. displacement graph is the work done by the force. Consider the situation of a block being pulled across a table with a constant force of 5 Newtons over a displacement of 5 meters, then the force gradually tapers off over the next 5 meters.
The work done by the force moving the block can be calculated by taking the area under the force vs. displacement graph (a combination of a rectangle and triangle) as follows:

FBD’s and Newton’s 2nd Law



Intro to Dynamics
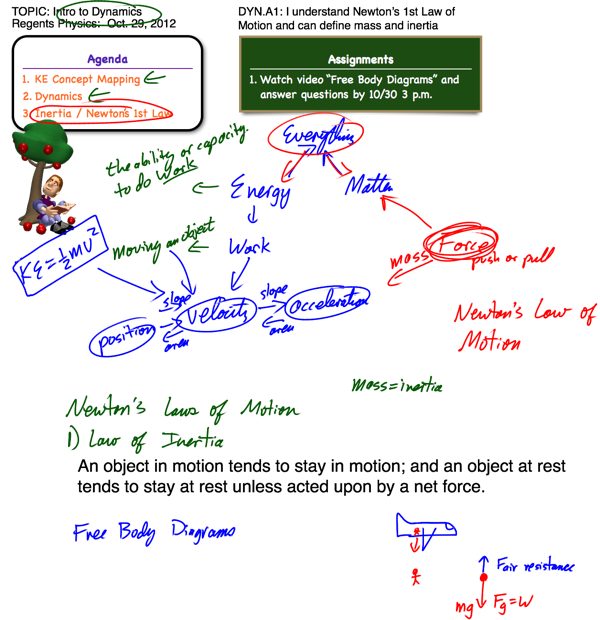
Newton’s 1st Law
Newton’s 1st Law of Motion, also known as the law of inertia, can be summarized as follows:
“An object at rest will remain at rest, and an object in motion will remain in motion, at constant velocity and in a straight line, unless acted upon by a net force.”
This means that unless there is a net (unbalanced) force on an object, an object will continue in its current state of motion with a constant velocity. If this velocity is zero (the object is at rest), the object will continue to remain at rest. If this velocity is not zero, the object will continue to move in a straight line at the same speed. However, if a net (unbalanced) force does act on an object, that object’s velocity will be changed (it will accelerate).

This sounds like a simple concept, but it can be quite confusing because it is difficult to observe this in everyday life. We’re usually fine with understanding the first part of the law: “an object at rest will remain at rest unless acted upon by a net force.” This is easily observable. The donut sitting on your breakfast table this morning didn’t spontaneously accelerate up into the sky. Nor did the family cat, Whiskers, lounging sleepily on the couch cushion the previous evening, all of a sudden accelerate sideways off the couch for no apparent reason.
The second part of the law contributes a considerably bigger challenge to our conceptual understandings. Realizing that “an object in motion will continue in its current state of motion with constant velocity unless acted upon by a net force” isn’t easy to observe here on Earth, making this law rather tricky. Almost all objects we observe in our everyday lives that are in motion are being acted upon by a net force – friction. Try this example: take your physics book and give it a good push along the floor. As expected, the book moves for some distance, but rather rapidly slides to a halt. An outside force, friction, has acted upon it. Therefore, from our typical observations, it would be easy to think that an object must have a force continually applied upon it to remain in motion. However, this isn’t so. If we took the same book out into the far reaches of space, away from any gravitational or frictional forces, and pushed it away from us, it would continue moving in a straight line at a constant velocity forever and ever, as there are no external forces to change its motion. When the net force on an object is 0, we say the object is in “static equilibrium.” We’ll revisit static equilibrium when we talk about Newton’s 2nd Law.
Inertia

The tendency of an object to resist a change in velocity is known as the object’s inertia. For example, a train has significantly more inertia than a skateboard. It is much harder to change the train’s velocity than it is the skateboard’s. The measure of an object’s inertia is its mass. For the purposes of this course, inertia and mass mean the same thing – they are synonymous.
And if you recall from the kinematics unit, a change in velocity is known as an acceleration. Therefore, the second part of this law could be re-written to state that an object acted upon by a net force will be accelerated. A more detailed description of this acceleration is given by Newton’s 2nd Law.
Forces

But, what exactly is a force? A force is a vector quantity describing the push or a pull on an object. Forces are measured in Newtons (N), named after Sir Isaac Newton, of course. A Newton is not a base unit, but is instead a derived unit, equivalent to 1 kg×m/s2. Interestingly, the gravitational force on a medium-sized apple is approximately 1 Newton.

We can break forces down into two basic types: contact forces and field forces. Contact forces occur when objects touch each other. Examples of contact forces include pushing a crate (applied force), pulling a wagon with a rope (tension force), a frictional force slowing down your sled, or even the force of air accelerating a spitwad through a straw. Field forces, also known as non-contact forces, occur at a distance. Examples of field forces include the gravitational force, the magnetic force, and the electrical force between two charged objects.

So, what then is a net force? A net force is just the vector sum of all the forces acting on an object. Imagine you and your sister are fighting over the last piece of licorice. You are pulling one end of the licorice toward you with a force of 5N. Your sister is pulling the other end toward her (in the opposite direction) with a force of 5N. The net force on the licorice, then, would be 0N, therefore there would be no net force. As it turns out, though, you have a passion for licorice, and now increase your pulling force to 6N. The net force on the licorice now is 1N in your direction, therefore the licorice would begin to accelerate toward you (yippee!) If it’s starting to sound complicated, it can be difficult to keep track of all the forces acting on an object just by writing those forces in words.
Free Body Diagrams
Fortunately, we have a terrific tool for helping us to analyze the forces acting upon objects. This tool is known as a free body diagram. Quite simply, a free body diagram is just a representation of a single object, or system, with vector arrows showing all the external forces acting on the object. These diagrams make it very easy to identify exactly what the net force is on an object, and they’re also quite simple to create:
- Isolate the object of interest. Draw the object as a point particle representing the same mass.
- Sketch and label each of the external forces acting on the object.
- Choose a coordinate system, with the direction of motion as one of the positive coordinate axes.
- If all forces do not line up with your axes, resolve those forces into componentsusing trigonometry.
- Redraw your free body diagram, replacing forces that don’t overlap the coordinates axes with their components.

As an example, let’s picture the example of an ice cream sundae, with whipped cream and chocolate sprinkles, sitting on the dining room table. We can represent our object (the ice cream sundae) in the diagram as a single dot. Then, we represent each of the vector forces acting on the sundae by drawing arrows and labeling them. In this case, we can start by recognizing the force of gravity on the sundae, known as the sundae’s weight. Although we could label this force as Fgrav, or W, we’ll get in the habit right now of writing the force of gravity on an object as mg. We can do this because the force of gravity on an object is equal to the object’s mass times the acceleration due to gravity, g.

Of course, since the sundae isn’t accelerating, there must be another force acting on the sundae to balance out the weight. This force, the force of the table pushing up on the sundae, is known as the Normal Force (FN). In physics, the normal force refers to a force perpendicular to a surface (normal in this case meaning perpendicular). The force of gravity on the sundae must exactly match the normal force on the sundae, although they are in opposite directions, therefore there is no net force on the sundae. The free body diagram for this situation would look like this:
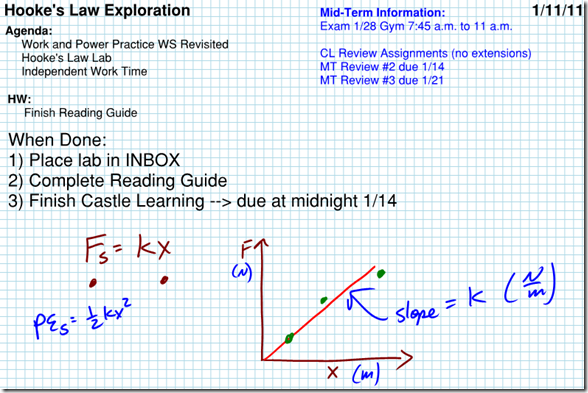
Hooke’s Law Lab
Hooke’s Law
An interesting application of work combined with the Force and Displacement graph is examining the force applied by a spring. The more you stretch a spring, the greater the force of the spring… similarly, the more you compress a spring, the greater the force. This can be modeled as a linear relationship, where the force applied by the spring is equal to some constant time the displacement of the spring. Written mathematically:
![]()
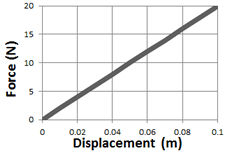
F is the force of the spring in newtons, x is the displacement of the spring from its equilibrium (or rest) position, in meters, and k is the spring constant which tells you how stiff or powerful a spring is, in Newtons per meter. The larger the spring constant, k, the more force the spring applies per amount of displacement.
You can determine the spring constant of a spring by making a graph of the force from a spring on the y-axis, and placing the displacement of the spring from its equilibrium, or rest position, on the x-axis. The slope of the graph will give you the spring constant. For the case of the spring depicted in the graph at right, we can find the spring constant as follows:
![]()
You must have done work to compress or stretch the spring, since you applied a force and caused a displacement. How can you find the work done in stretching or compressing the spring? By taking the area under the graph. For the spring shown, to displace the spring 0.1m, we can find the work done as shown:
![]()
Intro to Work and Power
Defining Work
Sometimes we work hard. Sometimes we’re slackers. But, right now, are you doing work? And what do we mean by work?
Work — the process of moving an object by applying a force
In order for a force to qualify as having done work on an object, there must be a displacement and the force must cause the displacement.
I’m sure you can think up countless examples of work being done, but a few that spring to my mind include pushing a snowblower to clear the driveway, pulling a sled up a hill with a rope, stacking boxes of books from the floor onto a shelf, and throwing a baseball from the pitcher’s mound to home plate.
Let’s try an exercise: Which of the following are examples of work being done?

- Sandy struggles to push her stalled car, but can’t make it move.
- Jeeves the butler carries a tray above his head by one arm across the room at a constant velocity.
- A missile streaks through the upper atmosphere.
Each of these examples help us better understand the definition of work. In example 1, even though Sandy pushes her car, with all her might, the car doesn’t move, therefore no work is done.
Example 2 is a very tricky situation. In this scenario, Jeeves applies a force upward with his arm, but the tray moves horizontally. From this perspective, the force of the butler’s arm isn’t causing the displacement, therefore you could say no work is done by his arm. However, Jeeves’ legs are pushing him forward, and therefore the tray moves horizontally, so you could say from this perspective he is doing work on the tray. (In actuality, the situation is even more complex than this as we pull friction and normal forces into the equation, but for the sake of clarity, let’s move on…)

In example 3, the missile’s engines are applying a force causing it to move. But what is doing the work? The hot expanding gas is pushed backward out of the missile’s engine… so, using Newton’s 3rd Law, we observe the reactionary force of the gas pushing the missile forward, causing a displacement. Therefore, the expanding exhausted gas is doing work on the missile!
Calculating Work
Mathematically, work can be expressed by the following equation:
![]()
Where W is the work done, F is the force applied, in Newtons, and d is the object’s displacement, in meters.
The units of work can be found by a unit analysis of the work formula. If work is force multiplied by distance, the units must be the units of force multiplied by the units of distance, or newtons multiplied by meters. A newton-meter is also known as a Joule (J).

It’s important to note that when using this equation, only the force applied in the direction of the object’s displacement counts! This means that if the force and displacement vectors aren’t in exactly the same direction, you need to take the component of force in the direction of the object’s displacement. To do this, line up the force and displacement vectors tail-to-tail and measure the angle between them. Since this component of force can be calculated by multiplying the force times the cosine of the angle between the force and displacement vectors, we can re-write our work equation as:
![]()
Let’s examine a few more examples:
Question: An appliance salesman pushes a refrigerator 2 meters across the floor by applying a force of 200N. Find the work done.
Answer: Since the force and displacement are in the same direction, the angle between them is 0:
.
Question: A friend’s car is stuck on the ice. You push down on the car to provide more friction for the tires (by way of increasing the normal force), allowing the car’s tires to propel it forward 5m onto less slippery ground. How much work did you do?
Answer: You applied a downward force, yet the car’s displacement was sideways. Therefore, the angle between the force and displacement vectors is 90°, so:
.
Question: You push a crate up a ramp with a force of 10N. Despite your pushing, however, the crate slides down the ramp a distance of 4m. How much work did you do?
Answer: Since the direction of the force you applied is opposite the direction of the crate’s displacement, the angle between the two vectors is 180°.
Question: How much work is done in lifting an 8-kg box from the floor to a height of 2m above the floor?
Answer: It’s easy to see the displacement is 2m, and the force must be applied in the direction of the displacement, but what is the force? To lift the box we must match and overcome the force of gravity on the box. Therefore, the force we must apply is equal to the gravitational force, or weight, of the box:

Question:Barry, John, and Sidney pull a 30-kg wagon with a force of 500N a distance of 20m. The force acts at a 30° angle to the horizontal. Calculate the work done.
Answer:
Force vs. Displacement Graphs

The area under a force vs. displacement graph is the work done by the force. Consider the situation of a block being pulled across a table with a constant force of 5 Newtons over a displacement of 5 meters, then the force gradually tapers off over the next 5 meters.
The work done by the force moving the block can be calculated by taking the area under the force vs. displacement graph (a combination of a rectangle and triangle) as follows: