Tag Archives: free body diagrams
Free Body Diagrams


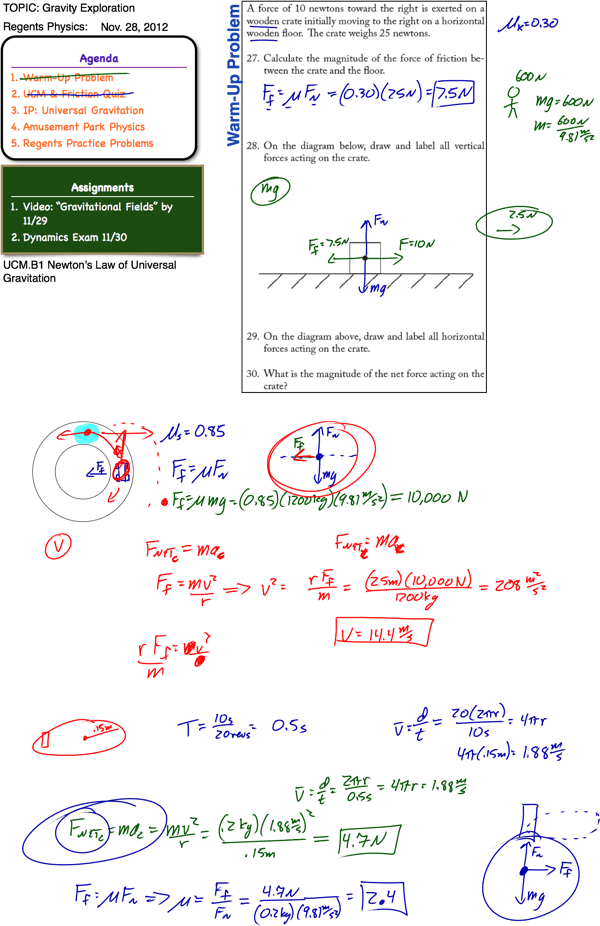
Gravity Exploration
Scales in Elevators


FBD’s and Newton’s 2nd Law



Intro to Dynamics
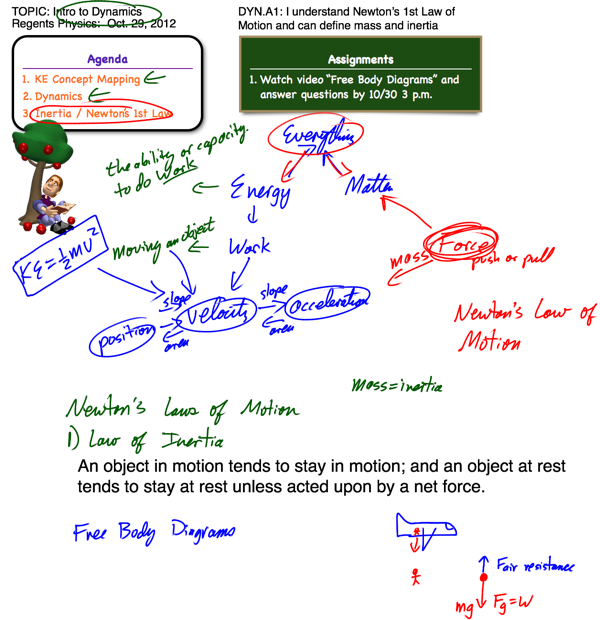
Newton’s 1st Law
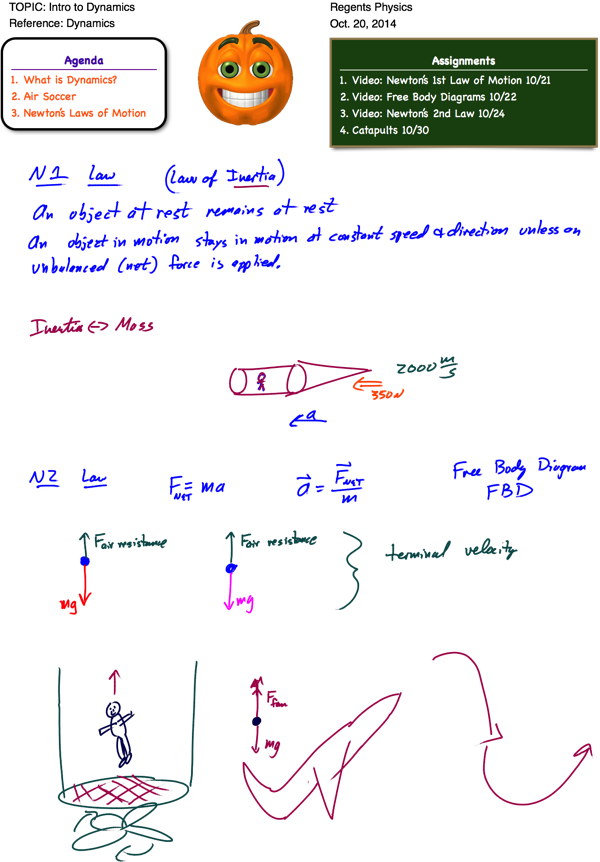
Newton’s 1st Law of Motion, also known as the law of inertia, can be summarized as follows:
“An object at rest will remain at rest, and an object in motion will remain in motion, at constant velocity and in a straight line, unless acted upon by a net force.”
This means that unless there is a net (unbalanced) force on an object, an object will continue in its current state of motion with a constant velocity. If this velocity is zero (the object is at rest), the object will continue to remain at rest. If this velocity is not zero, the object will continue to move in a straight line at the same speed. However, if a net (unbalanced) force does act on an object, that object’s velocity will be changed (it will accelerate).

This sounds like a simple concept, but it can be quite confusing because it is difficult to observe this in everyday life. We’re usually fine with understanding the first part of the law: “an object at rest will remain at rest unless acted upon by a net force.” This is easily observable. The donut sitting on your breakfast table this morning didn’t spontaneously accelerate up into the sky. Nor did the family cat, Whiskers, lounging sleepily on the couch cushion the previous evening, all of a sudden accelerate sideways off the couch for no apparent reason.
The second part of the law contributes a considerably bigger challenge to our conceptual understandings. Realizing that “an object in motion will continue in its current state of motion with constant velocity unless acted upon by a net force” isn’t easy to observe here on Earth, making this law rather tricky. Almost all objects we observe in our everyday lives that are in motion are being acted upon by a net force – friction. Try this example: take your physics book and give it a good push along the floor. As expected, the book moves for some distance, but rather rapidly slides to a halt. An outside force, friction, has acted upon it. Therefore, from our typical observations, it would be easy to think that an object must have a force continually applied upon it to remain in motion. However, this isn’t so. If we took the same book out into the far reaches of space, away from any gravitational or frictional forces, and pushed it away from us, it would continue moving in a straight line at a constant velocity forever and ever, as there are no external forces to change its motion. When the net force on an object is 0, we say the object is in “static equilibrium.” We’ll revisit static equilibrium when we talk about Newton’s 2nd Law.
Inertia

The tendency of an object to resist a change in velocity is known as the object’s inertia. For example, a train has significantly more inertia than a skateboard. It is much harder to change the train’s velocity than it is the skateboard’s. The measure of an object’s inertia is its mass. For the purposes of this course, inertia and mass mean the same thing – they are synonymous.
And if you recall from the kinematics unit, a change in velocity is known as an acceleration. Therefore, the second part of this law could be re-written to state that an object acted upon by a net force will be accelerated. A more detailed description of this acceleration is given by Newton’s 2nd Law.
Forces

But, what exactly is a force? A force is a vector quantity describing the push or a pull on an object. Forces are measured in Newtons (N), named after Sir Isaac Newton, of course. A Newton is not a base unit, but is instead a derived unit, equivalent to 1 kg×m/s2. Interestingly, the gravitational force on a medium-sized apple is approximately 1 Newton.

We can break forces down into two basic types: contact forces and field forces. Contact forces occur when objects touch each other. Examples of contact forces include pushing a crate (applied force), pulling a wagon with a rope (tension force), a frictional force slowing down your sled, or even the force of air accelerating a spitwad through a straw. Field forces, also known as non-contact forces, occur at a distance. Examples of field forces include the gravitational force, the magnetic force, and the electrical force between two charged objects.

So, what then is a net force? A net force is just the vector sum of all the forces acting on an object. Imagine you and your sister are fighting over the last piece of licorice. You are pulling one end of the licorice toward you with a force of 5N. Your sister is pulling the other end toward her (in the opposite direction) with a force of 5N. The net force on the licorice, then, would be 0N, therefore there would be no net force. As it turns out, though, you have a passion for licorice, and now increase your pulling force to 6N. The net force on the licorice now is 1N in your direction, therefore the licorice would begin to accelerate toward you (yippee!) If it’s starting to sound complicated, it can be difficult to keep track of all the forces acting on an object just by writing those forces in words.
Free Body Diagrams
Fortunately, we have a terrific tool for helping us to analyze the forces acting upon objects. This tool is known as a free body diagram. Quite simply, a free body diagram is just a representation of a single object, or system, with vector arrows showing all the external forces acting on the object. These diagrams make it very easy to identify exactly what the net force is on an object, and they’re also quite simple to create:
- Isolate the object of interest. Draw the object as a point particle representing the same mass.
- Sketch and label each of the external forces acting on the object.
- Choose a coordinate system, with the direction of motion as one of the positive coordinate axes.
- If all forces do not line up with your axes, resolve those forces into componentsusing trigonometry.
- Redraw your free body diagram, replacing forces that don’t overlap the coordinates axes with their components.

As an example, let’s picture the example of an ice cream sundae, with whipped cream and chocolate sprinkles, sitting on the dining room table. We can represent our object (the ice cream sundae) in the diagram as a single dot. Then, we represent each of the vector forces acting on the sundae by drawing arrows and labeling them. In this case, we can start by recognizing the force of gravity on the sundae, known as the sundae’s weight. Although we could label this force as Fgrav, or W, we’ll get in the habit right now of writing the force of gravity on an object as mg. We can do this because the force of gravity on an object is equal to the object’s mass times the acceleration due to gravity, g.

Of course, since the sundae isn’t accelerating, there must be another force acting on the sundae to balance out the weight. This force, the force of the table pushing up on the sundae, is known as the Normal Force (FN). In physics, the normal force refers to a force perpendicular to a surface (normal in this case meaning perpendicular). The force of gravity on the sundae must exactly match the normal force on the sundae, although they are in opposite directions, therefore there is no net force on the sundae. The free body diagram for this situation would look like this:

