Uniform Circular Motion

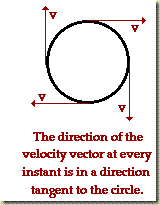
Question: Is a car moving at a constant speed around a circular track accelerating?

Yes. Why? It’s velocity is constantly changing, because velocity has a direction. Since acceleration is a change in velocity, the car must be accelerating.

CENTRIPETAL ACCELERATIONS

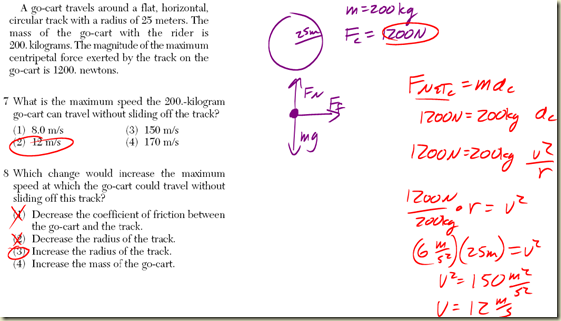
Centripetal acceleration is a vector quantity directed toward the center of curvature. Its magnitude is calculated from ac=v2/r.

When an object moves in a circle, its velocity is constantly changing. This changing in direction indicates that the object is being accelerated. Since velocity is a vector quantity, any change in magnitude (speed) or direction indicates acceleration.

Since we’re already talking about acceleration, we can relate this directly to Newton’s 2nd Law… F=ma. If we can have a centripetal, or center-seeking, acceleration, we must also have a centripetal center-seeking force.

Fc=mac=mv2/r

Note that centripetal force is just a generic name for any force that is pulling something toward the center of a radius of curvature, it is NOT some new magical force that appears — it must be caused by something such as a rope, gravity, friction, etc.

When the source of the centripetal force is removed, the object will move in a straight line tangent to the circle.







Uniform circular motion, or motion at a constant speed, is only one of the many types of circular motion.

We already know, from our kinematics, that for an object going in a circular path at a constant acceleration,



And circumference is C=2πr. Combining these two equations, then, we get



where T is the period, or the time it takes for the object to make one cycle around the circle.

Period (T) = time it takes for an object to go around the circle one time.

Let’s look at the velocity of an object in uniform circular motion:

We can describe the velocity vector of an object in uniform circular motion as being tangential.

Frequency (f) = number of revolutions per second.

T=1/f (measured in Hz)