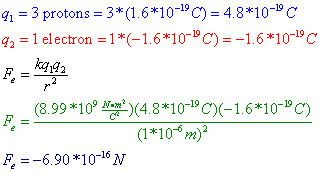Tag Archives: conservation of charge
Electric Charge
Charge Sensing Lab
Conduction and Induction
Intro to Circuit Analysis
An electrical circuit is a closed loop path through which current can flow. An electrical circuit can be made up of almost any materials (including humans if we’re not careful!), but practically speaking, they are typically comprised of electrical devices such as wires, batteries, resistors, and switches. Conventional current will flow through a complete closed-loop path (closed circuit) from high potential to low potential, therefore electrons actually flow in the opposite direction, from low potential to high potential. If there the path isn’t a closed loop (open circuit), no charge will flow.
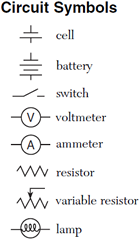
Electric circuits, which are three-dimensional constructs, are typically represented in two dimensions using diagrams known as circuit schematics. These schematics are simplified, standardized representations in which common circuit elements are represented with specific symbols, and wires connecting the elements in the circuit are represented by lines. Basic circuit schematic symbols are shown in the Physics Reference Table.
In order for current to flow through a circuit, you must have a source of potential difference. Typical sources of potential difference are voltaic cells, batteries (which are just two or more cells connected together), and power (voltage) supplies. We often times refer to voltaic cells as batteries in common terminology. In drawing a cell or battery on a circuit schematic, remember that the longer side of the symbol is the positive terminal.
Electric circuits must form a complete conducting path in order for current to flow. In the example circuit shown below left, the circuit is incomplete because the switch is open, therefore no current will flow and the lamp will not light. In the circuit below right, however, the switch is closed, creating a closed loop path. Current will flow and the lamp will light up.
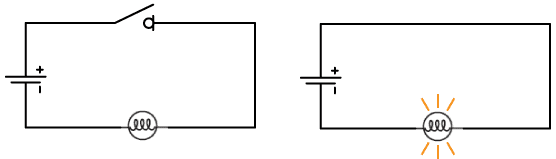
Note that in the picture at right, conventional current will flow from positive to negative, creating a clockwise current path in the circuit. The actual electrons in the wire, however, are flowing in the opposite direction, or counter-clockwise.
Kirchhoff’s Laws
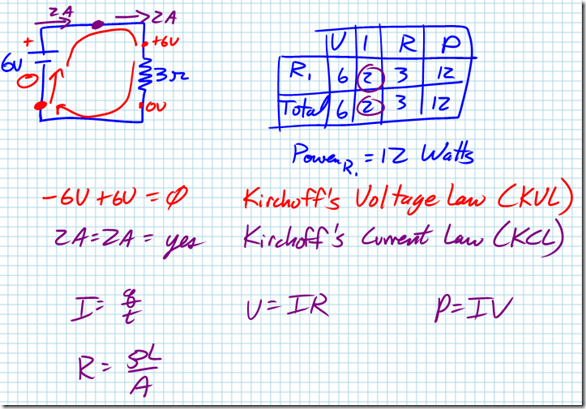
Kirchhoff’s Current Law (KCL), named after German physicist Gustav Kirchhoff, states that the sum of all current entering any point in a circuit has to equal the sum of all current leaving any point in a circuit. More simply, this is another way of looking at the law of conservation of charge.
Kirchhoff’s Voltage Law (KVL) states that the sum of all the potential drops in any closed loop of a circuit has to equal zero. More simply, KVL is a method of applying the law of conservation of energy to a circuit.
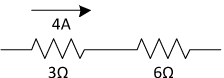
Question: A 3.0-ohm resistor and a 6.0-ohm resistor are connected in series in an operating electric circuit. If the current through the 3.0-ohm resistor is 4.0 amperes, what is the potential difference across the 6.0-ohm resistor?
Answer: First, let’s draw a picture of the situation. If 4 amps of current is flowing through the 3-ohm resistor, then 4 amps of current must be flowing through the 6-ohm resistor according to Kirchhoff’s Current Law. If we know the current and the resistance, we can calculate the voltage drop across the 6-ohm resistor using Ohm’s Law:
Charge Sensing Lab
Introduction
The work electricity comes from the Greek word elektron, which means "amber." Amber is a petrified tree resin, and the ancient Greeks understand that if you rub an amber rod with a piece of cloth, the amber attracts small pieces of leaves or dust. A piece of hard rubber, a glass rod, or a plastic ruler rubbed with a cloth can also display this "amber effect," which we know as static electricity.
Two types of electric charge exist, as determined by Benjamin Franklin in the 1700s. Franklin labeled these charges "positive" and "negative." He also found that the charges either attract each other, or repel each other. Detailed experiments showed that unlike charges attract, and like charges repel.
Franklin also determined that, in generating any amount of charge, the amount of charge generated on the rod was equal to the amount of opposite charge generated by the cloth. Stated more clearly in the law of conservation of electric charge: "the net amount of electric charge produced in any process is zero."
Precautions in Using the Charge Sensor
Modern synthetic shoes, fabrics, and plastic insulators readily accumulate stray static charges under moderately dry conditions, so care must be taken that the charges measured are those in the experiment, not those on the experimenter. Three simple precautions help:
- Experiments should be performed on a lab table with a square of heavy-duty aluminum foil connected to the grounding (black) lead of the sensor. Folding the edges under 1 cm keeps the clip from tearing the foil.
- Use a metal can as the conducting sensor body, insulated from the ground plane by an empty inverted glass jar or beaker.
- The experimenter should be connected by a grounding lead to the foil ground plane by a grounding bracelet or a strip of heavy-duty foil, folded over four times, wrapped around one wrist, and connected to the ground plane with a long clip lead.
Experimental Setup
- Begin by setting up your experimental apparatus as shown. Place a square of aluminum foil on your lab table, and connect it to the ground (black) lead of your charge sensor. Place your metal sensing can on top of a glass jar on the aluminum foil, and connect the sensing (red) lead of the charge sensor to the can. Verify the charge sensor is set to +/- 10V. Press and hold the reset button the charge sensor to drain the capacitor.
- Connect the charge sensor to the LabPro using the Analog1 input. Start up LoggerPro software and verify that the software is reading charge. Again reset the charge sensor.
- Create a grounding strap for the experimenter by folding a thin piece of aluminum foil over 4 times and wrapping it around your wrist. Connect this strap to the grounded aluminum foil square using a long clip lead.
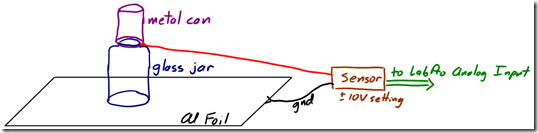
Detecting Charge by Induction
- Begin measurements by grounding the sensor and discharging the internal capacitor with the zero button. As you move through each step, record your observations.
- Rub a plastic straw or amber rod with a small square of paper towel, fur, or wool. Bring the straw or rod near the can and observe the reading.
- Observe the charge reading as you slowly lower the charged end of the straw or rod into the can.
- Rub the straw or rod lightly with your fingers to neutralize its charge and bring it near the can to check. Rub it with the fur or cloth and drop the fur or cloth immediately into the can and observe the effect.
- Experiment and determine what combination of materials gives you the most negative charge. What were the materials and what was that negative charge?
- What combination of materials gives you the most positive charge? What were the materials and what was that positive charge?
- Zero your system. Rub the plastic straw with a cloth and drop it into the can. What is the charge on the can? Now quickly drop in the cloth. Now what is the charge on the can? What does this say about the law of conservation of electric charge? Where might any error or stray charge have been lost or gained?
- Search the internet for "charging by induction." Using what you learned doing the experiment and what you read, write a summary paragraph explaining what charging by induction means.
Analyzing the Electroscope
- Obtain an electroscope and neutralize it. Explain how you neutralized the electroscope.
- Create a negative charge on a straw or rod. Bring the rod near the electroscope. Record what happens. Explain why the electroscope behaves as it does.
- Move the rod away from the electroscope. Record what happens. Explain why the electroscope behaves as it does.
- Move the rod back to the electroscope again, this time touching the rod to the contact on the electroscope. What happens? Now what happens when you move the rod away? Why?
Experiments with Charged Tape
- Charge two pieces of transparent tape oppositely by stikcing the sticky side of one to the slide side of the other. Draw them lightly between your fingers to neutralize stray charge, then bring them near the can to check for neutrality.
- Separate the pieces of tape and observe what happens when you bring them near each other.
- Observe the charge readings as you bring each one near the can. Note the effect of distance as you move a piece of tape closer to the can and the competing effect of the two pieces of tape as you move them closer to and farther from the can. Record and explain your observations.
- Drop a piece of charged tape into the can without touching the can yourself. Compare the reading with the charged tape in the can to the maximum reading as you brought it closer to the can.
- Drop the oppositely charged tape in the can. If you have handled them carefully, the charges should nearly cancel.
- Charge different lengths of tape and determine the charge per unit length (in nC per cm). Record your observations and data.
Deliverables
Carefully answer all questions and requests proposed in this lab report on a separate sheet of paper with your name and period at the top. Each class member must turn in their own paper. This will require you to read the entire set of directions in detail.
Your paper should have three sections:
- Detecting Charge by Induction
- Analyzing the Electroscope
- Experiments with Charged Tape
Place your neatly completed sheet in the Inbox.
Introduction to Electrostatics
Building Blocks of Matter
Matter is made up of atoms. Once thought to be the smallest building blocks of matter, we now know that atoms can be broken up into even smaller pieces, known as protons, electrons, and neutrons. Each atom consists of a dense core of positively charged protons and uncharged (neutral) neutrons. This core is known as the nucleus. It is surrounded by a “cloud” of much smaller, negatively charged electrons. These electrons orbit the nucleus in distinct energy levels. To move to a higher energy level, an electron must absorb energy. When an electron falls to a lower energy level, it gives off energy.
Most atoms are neutral — that is, they have an equal number of positive and negative charges, giving a net charge of 0. For this to occur, the number of protons must equal the number of electrons. In certain situations, however, an atom may gain or lose electrons. In these cases, the atom as a whole is no longer neutral, and we call it an ion. If an atom loses one or more electrons, it has a net positive charge, and is known as a positive ion. If, instead, an atom gains one or more electrons, it has a net negative charge, and is therefore called a negative ion. Like charges repel each other, while opposite charges attract each other. In physics, we represent the charge on an object with the symbol q.
Charge is a fundamental measurement in physics, much as length, time, and mass are fundamental measurements. The fundamental unit of charge is the Coulomb [C], which is a very large amount of charge. Compare that to the magnitude of charge on a single proton or electron, known as an elementary charge, which is equal to 1.6*10^-19 coulomb. It would take 6.25*10^18 elementary charges to make up a single coulomb of charge! (Don’t worry about memorizing these values, they’re listed for you on the front of the reference table!).
Question: An object possessing an excess of 6.0*10^6 electrons has what net charge?
Answer:
Conductors and Insulators
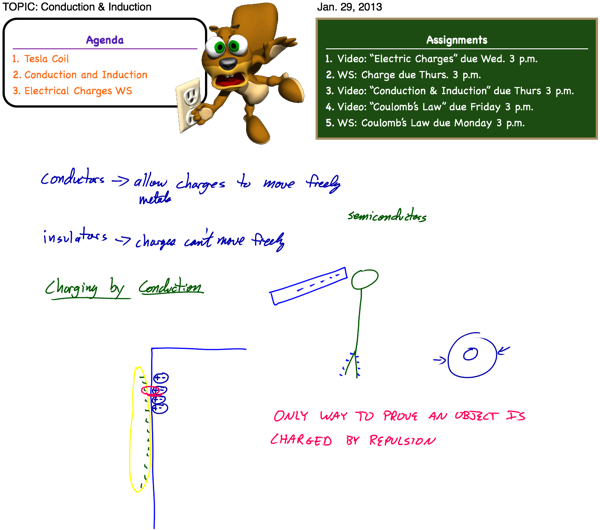
Certain materials allow electric charges to move freely. These are called conductors. Examples of good conductors include metals such as gold, copper, silver, and aluminum. In contrast, materials in which electric charges cannot move freely are known as insulators. Good insulators include materials such as glass, plastic, and rubber.
Conductors and insulators are characterized by their resistivity, or ability to resist movement of charge. Materials with high resistivities are good insulators. Materials with low resistivities are good conductors.
Semiconductors are materials which, in pure form, are good insulators. However, by adding small amounts of impurities known as dopants, their resistivities can be lowered significantly until they become good conductors.
Charging by Conduction
Materials can be charged by contact, or conduction. If you take a balloon and rub it against your hair, some of the electrons from the atoms in your hair are transferred to the balloon. The balloon now has extra electrons, and therefore has a net negative charge. Your hair has a deficiency of electrons, therefore it now has a net positive charge.
Much like momentum and energy, charge is also conserved. Continuing our hair and balloon example, the magnitude of the net positive charge on your hair is equal to the magnitude of the net negative charge on the balloon. The total charge of the hair/balloon system remains zero (neutral). For every extra electron (negative charge) on the balloon, there is a corresponding missing electron (positive charge) in your hair. This known as the law of conservation of charge.
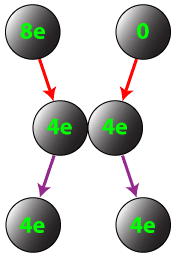
Conductors can also be charged by contact. If a charged conductor is brought into conduct with an identical neutral conductor, the net charge will be shared across the two conductors.
Question: If a conductor carrying a net charge of 8 elementary charges is brought into contact with an identical conductor with no net charge, what will be the charge on each conductor after they are separated?
Answer: Each conductor will have a charge of 4 elementary charges.
Question: What is the net charge (in coulombs) on each conductor after they are separated?
Answer:
Coulomb’s Law
We know that like charges repel, and opposite charges attract. In order for charges to repel or attract, they apply a force upon each either. Similar to the manner in which the force of attraction between two masses is determined by the amount of mass and the distance between the masses, as described by Newton’s Law of Universal Gravitation, the force of attraction or repulsion is determined by the amount of charge and the distance between the charges. The magnitude of the electrostatic force is described by Coulomb’s Law.
Coulomb’s Law states that the magnitude of the electrostatic force (Fe) between two objects is equal to a constant, k, multiplied by each of the two charges, q1 and q2, and divided by the square of the distance between the charges (r2). The constant k is known as the electrostatic constant, and is given on the reference table as: 
.
Notice how similar this formula is to the formula for the gravitational force! Both Newton’s Law of Universal Gravitation and Coulomb’s Law follow the inverse-square relationship, a pattern that repeats many times over in physics. The further you get from the charges, the weaker the electrostatic force. If you were to double the distance from a charge, you would quarter the electrostatic force on a charge.
Formally, a positive value for the electrostatic force indicates that the force is a repelling force, while a negative value for the electrostatic force indicates that the force is an attractive force. Because force is a vector, you must assign a direction to it. To determine the direction of the force vector, once you have calculated its magnitude, use common sense to tell you the direction on each charged object. If the objects have opposite charges, they are being attracted, and if they have like charges, they must be repelling each other.
Question: Three protons are separated from a single electron by a distance of 1*10^-6 m. Find the electrostatic force between them. Is this force attractive or repulsive?
Answer:
