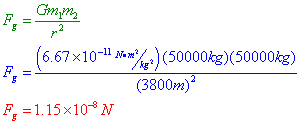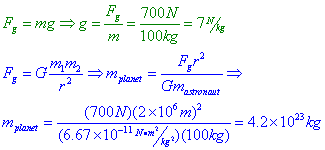Tag Archives: Newton’s Law of Universal Gravitation
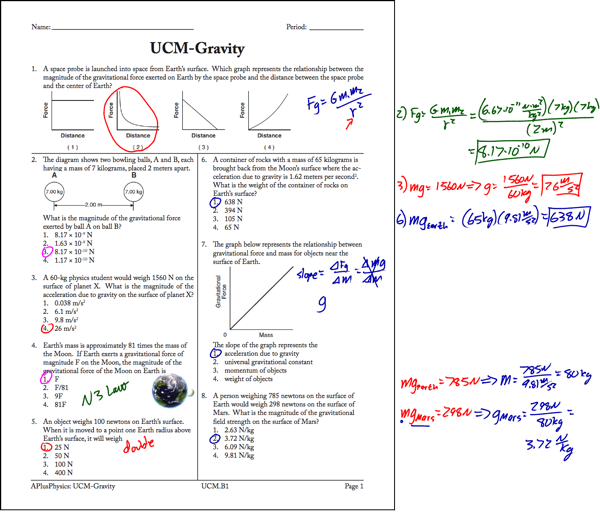
Regents Physics: Gravity Problem Solving Practice pp. 1 and 2
Gravitation
Agenda:
Interactive Physics: Gravity
Discussion: Gravitation, Grav. Fields, Orbits
Practice UCM & Grav Questions
HW:
Watch video: "Gravitational Fields" & answer ?s by Wednesday
Universal Gravitation
All objects that have mass attract each other with a gravitational force. The magnitude of that force, Fg, can be calculated using Newton’s Law of Universal Gravitation:
![]()
This law tells us that the force of gravity between two objects is proportional to each of the masses(m1 and m2) and inversely proportional to the square of the distance between them (r). The universal gravitational constant, G, is a "fudge factor," so to speak, included in the equation so that your answers come out in S.I. units. G is given on the front page of your Regents Physics Reference Table as ![]() .
.
Let’s look at this relationship in a bit more detail. Force is directly proportional to the masses of the two objects, therefore if either of the masses were doubled, the gravitational force would also double. In similar fashion, if the distance between the two objects, r, was doubled, the force of gravity would be quartered since the distance is squared in the denominator. This type of relationship is called an inverse square law, which describes many phenomena in the natural world.
NOTE: the distance between the masses, r, is actually the distance between the center of masses of the objects. For large objects, such as the Earth, for example, you must determine the distance to the center of the Earth, not to its surface.
Some hints for problem solving when dealing with Newton’s Law of Universal Gravitation:
- Substitute values in for variables at the very end of the problem only. The longer you can keep the formula in terms of variables, the fewer opportunities for mistakes.
- Before using your calculator to find an answer, try to estimate the order of magnitude of the answer. Use this to check your final answer.
- Once your calculations are complete, make sure your answer makes sense by comparing your answer to a known or similar quantity. If your answer doesn’t make sense, check your work and verify your calculations.
Let’s see if we can’t apply Newton’s Law of Universal Gravitation to a simple problem…
Question: What is the gravitational force of attraction between two asteroids in space, each with a mass of 50,000 kg, separated by a distance of 3800 m?
Answer:
As you can see, the force of gravity is a relatively weak force, and we would expect a relatively weak force between relatively small objects. It takes tremendous masses and small distances in order to develop significant gravitational forces. Let’s take a look at another problem to explore the relationships between gravitational force, mass, and distance.
Gravitational Fields
Gravity is a non-contact, or field, force. Its effects are observed without the two objects coming into contact with each other. Exactly how this happens is a mystery to this day, but scientists have come up with a mental construct to help us understand how gravity works.
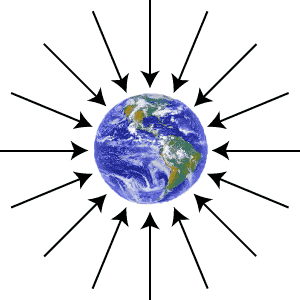
Envision an object with a gravitational field, such as the planet Earth. The closer other masses are to Earth, the more gravitational force they will experience. We can characterize this by calculating the amount of force the Earth will exert per unit mass at various distances from the Earth. Obviously, the closer the object is to the Earth, the larger a force it will experience, and the farther it is from the Earth, the smaller a force it will experience.
Attempting to visualize this, picture the strength of the gravitational force on a test object represented by a vector at the position of the object. The denser the force vectors are, the stronger the force, the stronger the "gravitational field." As these field lines become less and less dense, the gravitational field gets weaker and weaker.
To calculate the gravitational field strength at a given position, we can go back to our definition of the force of gravity on our test object, better known as its weight. We’ve been writing this as mg since we began our study of Dynamics. But, realizing that this is the force of gravity on an object, we can also calculate the force of gravity on test mass using Newton’s Law of Universal Gravitation. Putting these together we find that:
![]()
Realizing that the mass on the left-hand side of the equation, the mass of our test object, is also one of the masses on the right-hand side of the equation, we can simplify our expression by dividing out the test mass.
![]()
Therefore, the gravitational field strength, g, is equal to the universal gravitational constant, G, times the mass of the object, divided by the square of the distance between the objects.
But wait, you might say… I thought g was the acceleration due to gravity on the surface of the Earth! And you would be right. Not only is g the gravitational field strength, it’s also the acceleration due to gravity. The units even work out… the units of gravitational field strength, N/kg, are equivalent to the units for acceleration, m/s2!
Still skeptical? Let’s calculate the gravitational field strength on the surface of the Earth, using the knowledge that the mass of the Earth is approximately 5.98*1024 kg, and the distance from the surface to the center of mass of the Earth (which varies slightly since the Earth isn’t a perfect sphere) is approximately 6378 km in New York.
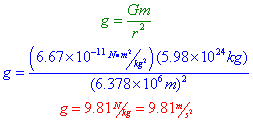
As expected, the gravitational field strength on the surface of the Earth is the acceleration due to gravity. Let’s see if we can’t solve some problems using gravitational field strength.
Question: Suppose a 100-kg astronaut feels a gravitational force of 700N when placed in the gravitational field of a planet.
A) What is the gravitational field strength at the location of the astronaut?
B) What is the mass of the planet if the astronaut is 2*106 m from its center?
Answer:
Electricity Refresher Solutions
Electric Field
Notes: Electrostatics Exam for P1, 4, 7 on 2/11; Exam for P8/9 on 2/10.
Electric Fields
Also similar to gravity, the electrostatic force is a non-contact force. Charged objects do not have to be in contact with each other to exert a force on each other. Somehow, a charged object feels the effect of another charged object through space. The property of space that allows a charged object to feel a force is a concept called electric field. Although we cannot see an electric field, we can detect its presence by placing a positive test charge at various points in space and measuring the force the test charge feels.
While looking at gravity, the gravitational field strength was the amount of force obsered by a mass per unit mass. The electric field strength is the amount of electrostatic force observed by a charge per unit charge. Therefore, the electric field strength, E, is the electrostatic force observed at a given point in space divided by the test charge itself. Electric field strength is measured in Newtons per Coulomb (N/C).
![]()
Electric Field Lines
Since we can’t actually see the electric field, we can draw electric field lines to help us visualize the force a charge would feel if placed at a specific position in space. To help us visualize the electric field, we can draw electric field lines in space. These lines show the direction a positive charged particle would feel a force if it were placed at that point in space. The more dense the lines are, the stronger the force a charged particle would feel, therefore the stronger the electric field. As the lines get further apart, the strength of the electric force a charged particle would feel is smaller, therefore the electric field is smaller.
By convention, we draw electric field lines showing the direction of force on a positive charge. Therefore, to draw electric field lines for a system of charges, follow these basic rules:
- Electric field lines point away from positive charges, and toward negative charges.
- Electric field lines never cross.
- Electric field lines always intersect conductors at right angles to the surface.
- Stronger fields have closer lines.
- Field strength and line density decreases as you move away from the charges.
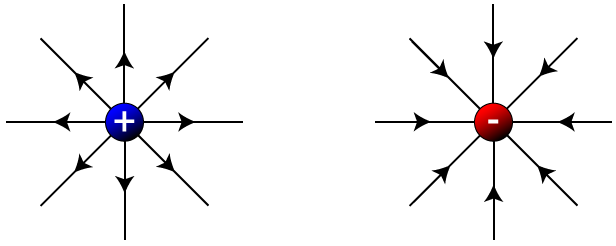
Let’s take a look at a few examples of electric field lines, starting with isolated positive (left) and negative (right) charges. Notice that for each charge, the lines radiate outward or inward spherically. The lines point away from the positive charge, since a positive test charge placed in the field (near the fixed charge) would feel a repelling force. The lines point in toward the negative fixed charge, since a positive test charge would feel an attractive force.
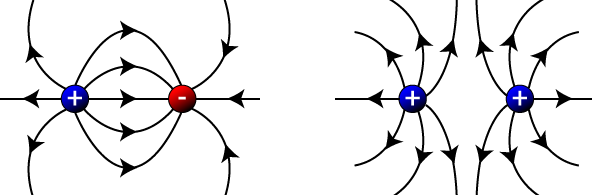
If you have both positive and negative charges in close proximity, you follow the same basic procedure:
Comparing Electrostatics & Gravity
Because gravity and electrostatics have so many similarities, let’s take a minute to do a quick comparison of electrostatics and gravity.
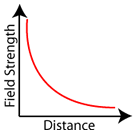
The big difference between electrostatics and gravity? The gravitational force can only attract, while the electrostatic force can both attract and repel. Notice again that both the electric field strength and the gravitational field strength follow the inverse-square law relationship. Field strength is inversely related to the square of the distance.