Tag Archives: Pythagorean Theorem

Quantities in physics are used to represent real-world measurements, and therefore physicists use these quantities as tools to better understand the world.  In examining these quantities, there are times when just a number, with a unit, can completely describe a situation.  These numbers, which have a magnitude, or size, only are known as scalars.  Examples of scalars include quantities such as temperature, mass, and time.  At other times, a quantity is more descriptive if it also includes a direction.  These quantities which have both a magnitude and direction are known as vectors.  Vector quantities you may be familiar with include force, velocity, and acceleration.

Most students will be familiar with scalars, but to many, vectors may be a new and confusing concept.  By learning just a few rules for dealing with vectors, though, you’ll find that they are a powerful tool for problem solving.

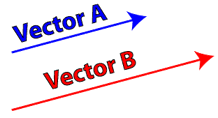
Vectors are often represented as arrows, with the length of the arrow indicating the magnitude of the quantity, and the direction of the arrow indicating the direction of the vector.  In the figure at right, vector B has a magnitude greater than that of vector A.  Vectors A and B point in the same direction, however.  It’s also important to note that vectors can be moved anywhere in space.  The positions of A and B could be reversed, and the individual vectors would retain their values of magnitude and direction.  This makes adding vectors very straightforward!

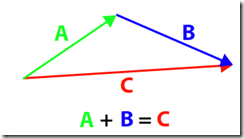To add vectors A and B, all we have to do is line them up so that the tip of the first vector touches the tail of the second vector.  Then, to find the sum of the vectors, known as the resultant, all we have to do is draw a straight line from the start of the first vector to the end of the last vector.  This method works with any number of vectors.

So then, how do we subtract two vectors?  Let’s try it by subtracting B from A. We could rewrite the expression A – B as A + -B.  Now it becomes an addition problem, we just have to figure out how to express –B.  This is easier than it sounds – to find the opposite of a vector, we just point the vector in the opposite direction.  Therefore, we can use what we already know about the addition of vectors to find the resultant of A–B.

Components of Vectors

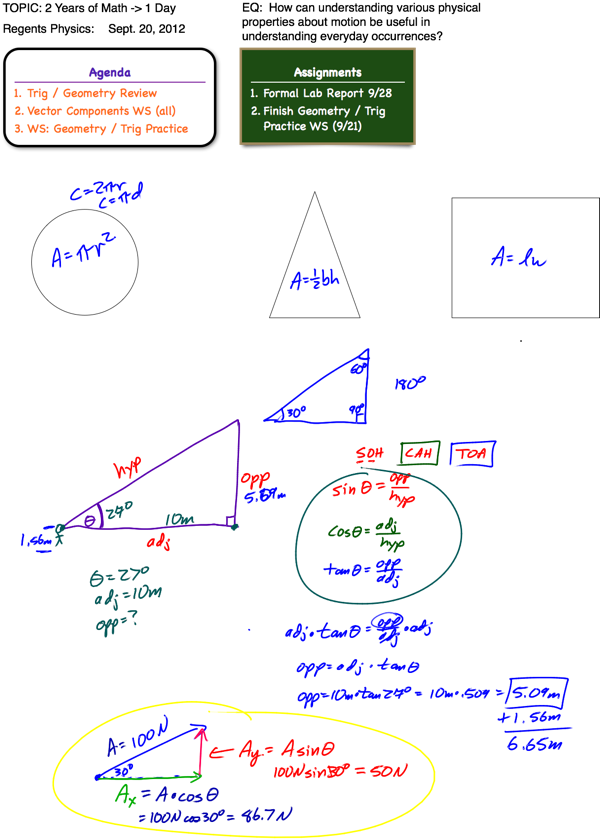
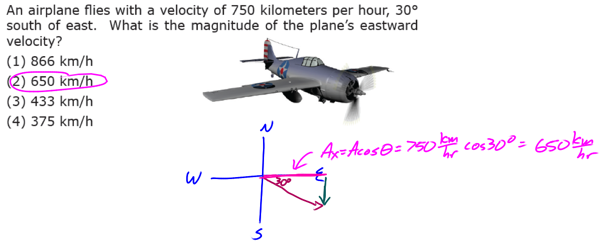
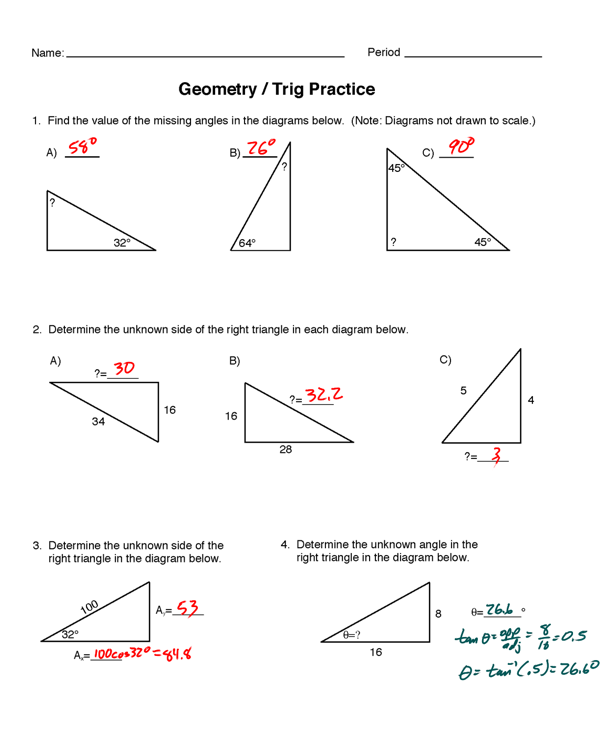
We’ll learn more about vectors as we go, but before we move on, there’s one more skill we need to learn. Vectors at angles can be challenging to deal with. By transforming a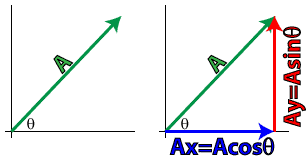 vector at an angle into two vectors, one parallel to the x-axis and one parallel to the y-axis, we can greatly simplify problem solving.  To break a vector up into its components, we can use our basic trig functions. To help us out even further, the Regents Physics Reference Table includes the exact formulas we need to determine the x- and y-components of any vector if we know that vector’s magnitude and direction.

In similar fashion, we can use the components of a vector in order to build the original vector. Graphically, if we line up the component vectors tip-to-tail, the original vector runs from the starting point of the first vector to the ending point of the last vector. To determine the magnitude of the resulting vector algebraically, just apply the Pythagorean Theorem!