Mid-Term results have been compiled and published. In general, scores are right in line with performance within the last few years. The exam itself was styled after the Regents Exam which is given at the end of the school year, and included topics from all aspects of Newtonian Mechanics (roughly half of the Regents Exam). This included 46 multiple choice questions, and 25 open-ended, or “free response,” type questions. Students were given 180 minutes to complete the exam, as well as a formula sheet (Regents Physics Reference Table), and a ruler. Students were permitted the use of a scientific calculator.
Summary Data
Summary data from this year’s exam, along with the previous two years of data, are shown at right.  Average score on the exam, with a fairly generous curve, was 76%, compared to 73% in 2010 and 74% in 2009. Median score was 78%, two points higher than last year’s exam, and right in line with 2009 scores. Percentage of students scoring above 85%, considered “Mastery Level” by Regents Physics standards, was 25%, slightly lower than in 2010 and 2009, but passing percentage was 83%, several points higher than in past years. Even more promising is a glance at a histogram
Average score on the exam, with a fairly generous curve, was 76%, compared to 73% in 2010 and 74% in 2009. Median score was 78%, two points higher than last year’s exam, and right in line with 2009 scores. Percentage of students scoring above 85%, considered “Mastery Level” by Regents Physics standards, was 25%, slightly lower than in 2010 and 2009, but passing percentage was 83%, several points higher than in past years. Even more promising is a glance at a histogram 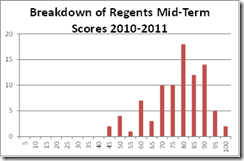 breaking down student scores further. This data indicates that we have many students in the 80-85% range. Past history has shown me that it is quite possible for students to improve their scores from 10-15% points between now and the actual Regents Exam in June with focused effort, study, and motivation. This indicates the potential for outstanding standardized exam performance in June if students buckle down and focus their efforts. Unfortunately, the Physics Regents Exam is usually one of the last tests offered (sometimes even after official graduation), so obtaining and maintaining student focus at this point of the year can be a challenge.
breaking down student scores further. This data indicates that we have many students in the 80-85% range. Past history has shown me that it is quite possible for students to improve their scores from 10-15% points between now and the actual Regents Exam in June with focused effort, study, and motivation. This indicates the potential for outstanding standardized exam performance in June if students buckle down and focus their efforts. Unfortunately, the Physics Regents Exam is usually one of the last tests offered (sometimes even after official graduation), so obtaining and maintaining student focus at this point of the year can be a challenge.
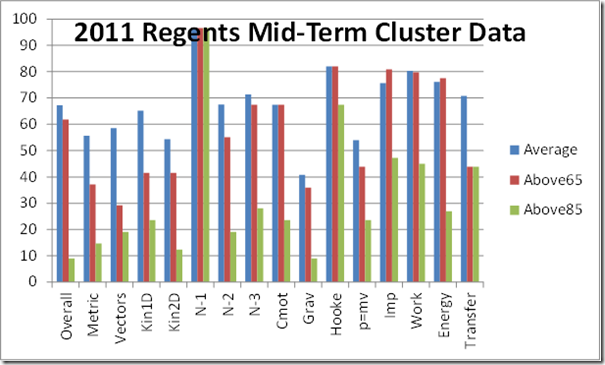
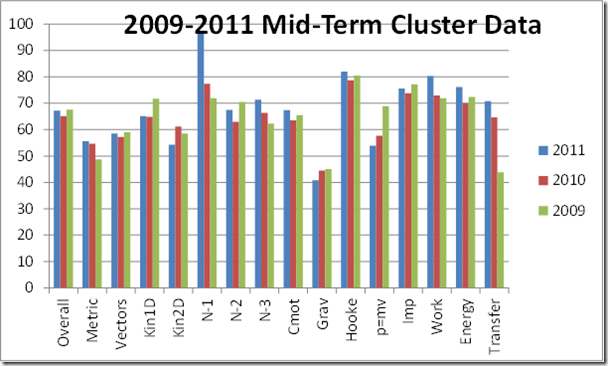
Cluster Data
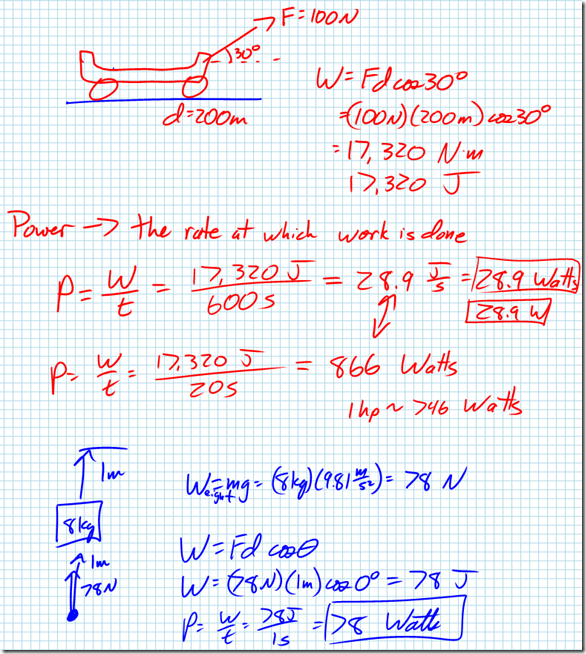
Breaking down exam performance by topic, we observe students demonstrating a very strong understanding of Newton’s Laws of Motion, Hooke’s Law (springs), and Work and Energy. These have been focus areas during the year, although there is room for further improvement in understanding Newton’s 2nd Law as well as momentum and impulse.
Cluster data indicates weaknesses in Newton’s Law of Universal Gravitation, although a deeper look at the questions and errors themselves indicates that most of the confusion here is a result of mathematical errors rather than conceptual misunderstandings. This is being re-emphasized as we work through Coulomb’s Law / Electrical Force problems, which utilize almost the exact same mathematical model. Other areas for improvement include 2-D Kinematics (projectile motion), a perennial challenge, and utilizing and understanding the metric system, a topic that has been emphasized and will continue to be reviewed throughout the year. Performance on momentum problems was, unsurprisingly, problematic. This relates directly to a “class as a whole” issue with independent practice and motivation throughout that unit, and will be our top priority for review in mid-June.
Conclusions
Student performance is in line with, if not slightly above, expectations for this point in the year. With a focused effort, students can fairly routinely increase their scores 10 to 15 percentage points by June. For struggling students, a variety of remediation protocols are being put in place, including the entire course content and sample quizzes available on the web, tailored directly to this course’s requirements (APlusPhysics.com), video lectures on topics corresponding directly to our textbook (Hippocampus), and even review sessions which can be viewed from any computer supporting iTunes (Windows, Mac, Linux, etc.) as well as iPods, iPhones, Blackberries, Android devices, etc. All of these resources are available both in the classroom as well as the school library for those who don’t have ready access to these resources outside of school.
Data has also been broken down to the same level for individual students, and will be utilized to develop both entire-class and individual review plans to allow students to focus on areas that will provide the biggest “bang for the buck” in their studies.