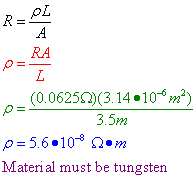
Tag Archives: wire
Mystery Circuit Challenge

LAB: Resistance of a Wire

WS: Resistance of a Wire
Resistance of a Wire
Resistance
Electrical charges can move easily in some materials (conductors) and less freely in others (insulators), as we learned previously. We describe a material’s ability to conduct electric charge as conductivity. Good conductors have high conductivities. The conductivity of a material depends on:
- Density of free charges available to move
- Mobility of those free charges
In similar fashion, we describe a material’s ability to resist the movement of electric charge using resistivity, symbolized with the Greek letter rho (![]() ). Resistivity is measured in ohm-meters, which are represented by the Greek letter omega multiplied by meters (
). Resistivity is measured in ohm-meters, which are represented by the Greek letter omega multiplied by meters (![]() •m). Both conductivity and resistivity are properties of a material.
•m). Both conductivity and resistivity are properties of a material.

When an object is created out of a material, the material’s tendency to conduct electricity, or conductance, depends on the material’s conductivity as well as the material’s shape. For example, a hollow cylindrical pipe has a higher conductivity of water than a cylindrical pipe filled with cotton. However, shape of the pipe also plays a role. A very thick but short pipe can conduct lots of water, yet a very narrow, very long pipe can’t conduct as much water. Both geometry of the object and the object’s composition influence its conductance.
Focusing on an object’s ability to resist the flow of electrical charge, we find that objects made of high resistivity materials tend to impede electrical current flow and have a high resistance. Further, materials shaped into long, thin objects also increase an object’s electrical resistance. Finally, objects typically exhibit higher resistivities at higher temperatures. We take all of these factors together to describe an object’s resistance to the flow of electrical charge. Resistance is a functional property of an object that describes the object’s ability to impede the flow of charge through it. Units of resistance are ohms (![]() ).
).
For any given temperature, we can calculate an object’s electrical resistance, in ohms, using the following formula, which can be found on your reference table.
![]()
In this formula, R is the resistance of the object, in ohms (![]() ), rho (
), rho (![]() ) is the resistivity of the material the object is made out of, in ohm*meters (
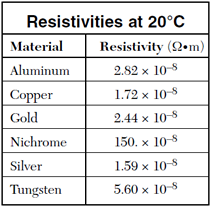
) is the resistivity of the material the object is made out of, in ohm*meters (![]() •m), L is the length of the object, in meters, and A is the cross-sectional area of the object, in meters squared. Note that a table of material resistivities for a constant temperature is given to you on the reference table!
•m), L is the length of the object, in meters, and A is the cross-sectional area of the object, in meters squared. Note that a table of material resistivities for a constant temperature is given to you on the reference table!
Let’s try a sample problem calculating the electrical resistance of an object:
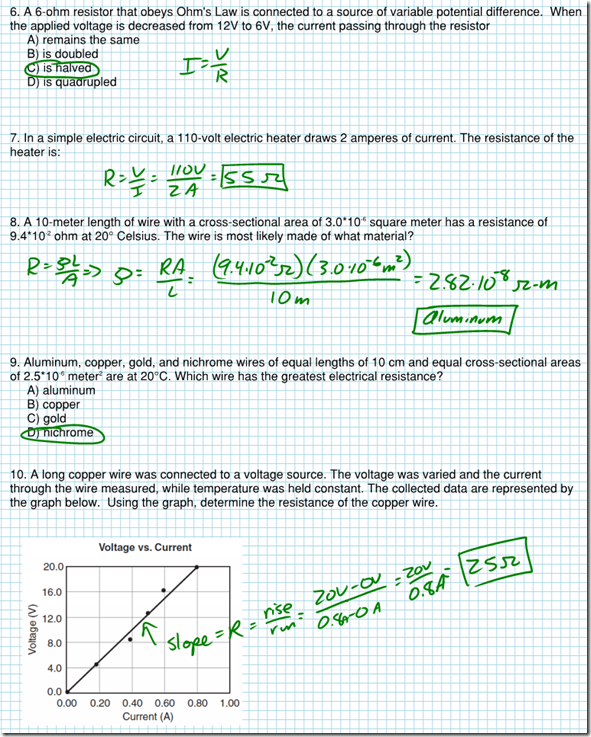
Question: A 3.50-meter length of wire with a cross-sectional
area of 3.14 × 10–6 m2 at 20° Celsius has a resistance of 0.0625. Determine the resistivity of the wire and the material it is made out of.
Answer: