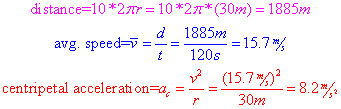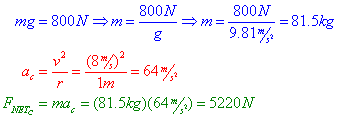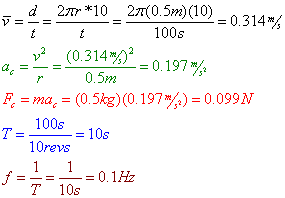Regents Physics - Uniform Circular Motion

Centripetal Acceleration

The motion of an object in a circular path at constant speed is known as uniform circular motion (UCM). An object in UCM is constantly changing direction, and since velocity is a vector and has direction, you could say that an object undergoing UCM has a constantly changing velocity, even if its speed remains constant. And if the velocity of an object is changing, it must be accelerating. Therefore, an object undergoing UCM is constantly accelerating. This type of acceleration is known as centripetal acceleration.

Question: If a car is accelerating, is its speed increasing?

Answer: It depends. Its speed could be increasing, or it could be accelerating in a direction opposite its velocity (slowing down). Or, its speed could remain constant yet still be accelerating if it is traveling in uniform circular motion.

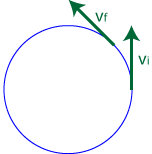
Just as importantly, we need to figure out the direction of the object's acceleration, since acceleration is a vector. To do this, let's draw an object moving counter-clockwise in a circular path, and show its velocity vector at two different points in time. Since we know acceleration is the rate of change of an object's velocity with respect to time, we can determine the direction of the object's acceleration by finding the direction of its change in velocity, Δv.

To find its change in velocity, Δv, we must recall that .

Therefore, we need to find the difference of the vectors v_f and v_i graphically, which can be re-written as .

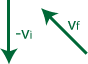
Recall that to add vectors graphically, we line them up, tip-to-tail, and then draw our resultant vector from the starting point (tail) of our first vector to the ending point (tip) of our last vector.

So, the acceleration vector must point in the direction shown above. If I show this vector back on our original circle, lined up directly between our initial and final velocity vector, it's easy to see that the acceleration vector points toward the center of the circle.

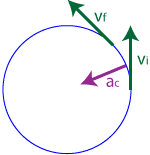
You can repeat this procedure from any point on the circle... no matter where you go, the acceleration vector always points toward the center of the circle. In fact, the word centripetal in centripetal acceleration means "center-seeking!"

So now we know the direction of an object's acceleration (toward the center of the circle), but what about its magnitude? Magnitude of an object's centripetal acceleration can be found on the reference table, and is given by the formula:

Circular Speed

So how do you find the speed of an object as it travels in a circular path? The formula for speed that we learned in kinematics still applies.

We have to be careful in using this equation, however, to understand that an object traveling in a circular path is traveling along the circumference of a circle. Therefore, if an object were to make one complete revolution around the circle, the distance it travels is equal to the circle's circumference.

Let's take a look at a sample problem:

Question: Miranda drives her car clockwise around a circular track of radius 30m. She completes 10 laps around the track in 2 minutes. Find Miranda's total distance traveled, average speed, and centripetal acceleration.

Answer:

Centripetal Force

If an object traveling in a circular path has an inward acceleration, Newton's 2nd Law tells us there must be a net force directed toward the center of the circle as well. This type of force, known as a centripetal force, can be a gravitational force, a tension, an applied force, or even a frictional force.

NOTE: When dealing with circular motion problems, it is important to realize that a centripetal force isn't really a new force, a centripetal force is just a label or grouping we apply to a force to indicate its direction is toward the center of a circle. This means that you never want to label a force on a free body diagram as a centripetal force, Fc. Instead, label the center-directed force as specifically as you can. If a tension is causing the force, label the force FT. If a frictional force is causing the center-directed force, label it Ff, and so forth.

We can combine the equation for centripetal acceleration with Newton's 2nd Law to obtain Newton's 2nd Law for Circular Motion. Recall that Newton's 2nd Law states:

For an object traveling in a circular path, there must be a net (centripetal) force directed toward the center of the circular path to cause a (centripetal) acceleration directed toward the center of the circular path. We can revise Newton's 2nd Law for this particular case, then, as follows:

Then, recalling our formula for centripetal acceleration as:

We can put these together, replacing a_c in our equation to get a combined form of Newton's 2nd Law for Uniform Circular Motion:

Of course, if an object is traveling in a circular path and the centripetal force is removed, the object will continue traveling in a straight line in whatever direction it was moving at the instant the force was removed.

Question: An 800N running back turns a corner in a circular path of r=1m at a velocity of 8 m/s. Find the running back's mass, centripetal acceleration, and centripetal force.

Answer: Given mg=800N, r=1m, v=8m/s; Find m, a_c, F_c

Let's try another one:

Another sample problem, this time involving only algebraic manipulation:

Frequency and Period

For objects moving in circular paths, we can characterize their motion around the circle using the terms frequency (f) and period (T). The frequency of an object is the number of revolutions the object makes in a complete second. It is measured in units of [1/s], or Hertz (Hz). In similar fashion, the period of an object is the time it takes to make one complete revolution. Since the period is a time interval, it is measured in units of seconds. We can relate period and frequency using the equations:

Question: A 500g toy train completes 10 laps of its circular track in 1 min 40s. If the diameter of the track is 1m, find the train's centripetal acceleration (a_c), centripetal force (F_c), period (T), and frequency (f).

Answer:

Let's look at another example:

Vertical Circular Motion

Objects travel in circles vertically as well as horizontally. Because the speed of these objects isn't typically constant, technically this isn't uniform circular motion, but our UCM analysis skills still prove applicable.

Consider a roller coaster traveling in a vertical loop of radius 10m. You travel through the loop upside down, yet you don't fall out of the roller coaster. How is this possible? We can use our understanding of UCM and dynamics to find out!

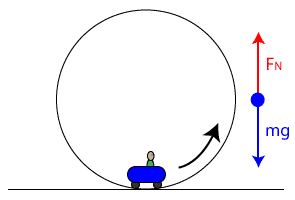
Bottom of the Circle

To begin with, let's first take a look at the coaster when the car is at the bottom of the loop. Drawing a free body diagram, the force of gravity on the coaster, also known as its weight, pulls it down, so we draw a vector pointing down labeled "mg." Opposing that force is the normal force of the rails of the coaster pushing up, which we label F_N.

Because the coaster is moving in a circular path, we can analyze it using the tools we developed for uniform circular motion. Newton's 2nd Law still applies, so we can write:

Notice that because we're talking about circular motion, we'll adopt the convention that forces pointing toward the center of the circle are positive, and forces pointing away from the center of the circle are negative. At this point, recall that the force you "feel" when you're in motion is actually the normal force. So, solving for the normal force as you begin to move in a circle, we find that

Since we know that the net force is always equal to mass times acceleration, so the net centripetal force is equal to mass times the centripetal acceleration, we can replace F_NETc as follows:

We can see from the resulting equation that the normal force is now equal to the weight plus an additional term from the centripetal force of the circular motion. As we travel in a circular path near the bottom of the loop, then, we feel heavier than our weight. In common terms, we feel additional "g-forces." How many g's we feel can be obtained with a little bit more manipulation. If we re-write our equation for the normal force, pulling out the mass by applying the distributive property of multiplication, we obtain:

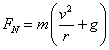
Notice that inside the parenthesis we have our standard acceleration due to gravity, g, plus a term from the centripetal acceleration (). This additional term is the additional g-force felt by a person. For example, if a_c was equal to g (9.81 m/s²), you could say the person in the cart was experiencing two g's (1g from the centripetal acceleration, and 1g from the Earth's gravitational field). If a_c were equal to 3×g (29.4 m/s²), the person would be experiencing a total of four g's.

Expanding this analysis to a similar situation in a different context, try to imagine instead of a roller coaster, a mass whirling in a vertical circle by a string. You could replace the normal force by the tension in the string in our analysis. Because the force is larger at the bottom of the circle, the likelihood of the string breaking is highest when the mass is at the bottom of the circle!

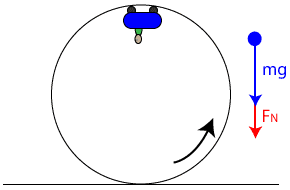
Top of the Circle

At the top of the loop, we have a considerably different picture. Now, the normal force from the coaster rails must be pushing down against the cart, though still in the positive direction since down is now toward the center of the circular path. In this case, however, the weight of the object also points toward the center of the circle, since the Earth's gravitational field always pulls toward the center of the Earth. Our free body diagram looks considerably different, and therefore our application to Newton's 2nd Law for Circular Motion is considerably different as well.

Since the force you feel is actually the normal force, we can solve for the normal force and expand the net centripetal force as shown:

You can see from the equation that the normal force is now the centripetal force minus your weight. If the centripetal force were equal to your weight, you would feel as though you were weightless. Note that this is also the point where the normal force is exactly equal to 0. This means the rails of the track are no longer pushing on the roller coaster cart... if the centripetal force were even the tiniest bit less (the car's speed was the tiniest bit less), the normal force F_N would be less than 0. Since the rails can't physically pull the cart in the negative direction (away from the center of the circle), this means the car is falling off the rail and the cart's occupant is about to have a very, very bad day. Only by maintaining a high speed can the cart successfully negotiate the loop... go too slow and the cart falls.

In order to remain safe, real roller coasters actually have wheels on both sides of the rails to prevent the cart from falling if it ever did slow down at the top of a loop, although coasters are designed so that this situation never actually occurs.