(You, of course, indicating its impact on the Earth and not necessarily you on a personal level.)

By essentially sapping energy from an orbital system, gravitational radiation makes orbits more circular and continuously decreases their radii. Overall angular momentum decreases, as this too is essentially stolen by radiation. The decrease in the radius of orbit is given by the following equation: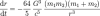

Substitution of the Earth's and Sun's masses for m1 and m2 tells us that the rate of our orbit with the Sun is decreasing by the second: 1.1 * 10^-20 meters per second, to be exact. Not to freak you out or anything, but we're getting closer and closer to the Sun as you read this. In exactly 365 days (that's a year in math terms), we will be MUCH closer to the Sun than we are now. About 1/300 of the diameter of a hydrogen atom. Now that's a bafflingly huge number, but I'm sure we have a few years left under our belt before we collapse into the Sun and die fiery deaths.

This equation can tell us the lifetime of an orbit as well, before this collapsing occurs. However, since the rate of change depends on the radius and not time, integration of the equation is necessary. So the lifetime of an orbital radius is brought to you by this guy here: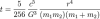

Again, substituting in the Earth's and Sun's masses, we find our orbit to be about 1.09 * 10^23 years. Seems pretty massive, especially considering this is 10^13 times larger than the age of the Universe itself.

Well, I hope you learned something, and I'll see you next quarter.