Winter Physics 2018-2: Ice Skating
The winter Olympics has both traditional figure skating, and speed skating as events. For this post I will focus more on the physics in Speed skating. First, how to go forward on ice skates. Since the friction between ice and sharp skates is almost zero you cannot simply just move, however, an ice skater must keep one foot in the direction of travel and push off the other at an angle from the first foot. This then creates forces in the x and y plane of the second skate, and it is the perpendicular force that pushes the skater forward.
Now for short track speed skating.
The radius of the turns in short track are much smaller than those of traditional speed skating so the skaters must than rely on their momentum from the straight portions of the track in order to go around the turns. Also, the lean seen above is caused by the centripetal acceleration of the skater around the turn.
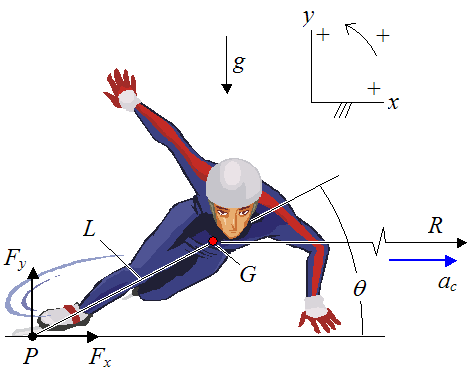
g= 9.8m/s2
G is the skaters center of mass
P is the point of contact between the skates and the ice
L is the distance between P and G
Fx and Fy are the x and y components of the contact force respectively
R is the turn radius
ac is the centripetal acceleration of the skater
Θ is the angle between L and the horizontal
Fy - mg = 0
Fx = m(v2/R)
Fx sinΘ *L - Fy sinΘ *L = 0
By combining the first and final equation you would end up with: tanΘ = (Rg)/(v2)
Assuming an average radius of 8m, and the top speed of American Olympian J.R. Celski, at around 10.967 m/s at the 2009 Jr championships, the angle that Celski would lead would be 33.1o


1 Comment
Recommended Comments