Regents Physics Free Fall

Definition: A free falling body is any object whose motion is affected only by gravity and moves vertically.

Conceptual Questions

1. If you were to hold an object in your hand and simply let go what happens to the object?
2. If you analyzed the motion of the object what might you notice? (hint: Think about what happens to the speed of the object.)

Background

Examination of free-falling bodies dates back to the days of Aristotle. At that time Aristotle believed that more massive objects would fall faster than less massive objects. He believed this in large part due to the fact that when examining a rock and a feather falling from the same height it is clear that the rock hits the ground first. Upon further examination it is clear that Aristotle was incorrect in his hypothesis. As proof take a basketball and a piece of paper. Drop them simultaneously from the same height… Do they land at the same time? Probably not…. Now take that piece of paper and crumple it up into a ball and repeat the experiment. Now what do you see happen? You should see that both the ball and the paper land at the same time. Therefore we can come to the conclusion that Aristotle's predictions did not account for the effect of air resistance. For the purposes of this course, we will neglect drag forces such as air resistance.

In the 17th century, Galileo Galilei began to extend the examination of the motion of falling bodies. Galileo, recognizing that air resistance affects the motion of a falling body, executed his famous thought experiment in which he continuously asked what would happen if the effect of air resistance was removed. Commander David Scott of Apollo 15 performed this experiment while on the moon. What do you notice about the time it takes for each object to hit the ground?

Since Galileo's experiments, scientists have come to a concrete understanding of how the gravitational pull of the Earth accelerates free-falling bodies. Through experimentation it has been found that on the surface of the Earth all objects experience acceleration (g) of 9.81 m/s².

NOTE: If we move off the surface of the Earth the acceleration due to gravity changes.

We can look at free-falling bodies as objects being dropped from some height or thrown vertically upward. In this examination we will analyze the motion of each condition.

Objects Dropped From Rest

Objects starting from rest have an initial velocity of zero, giving us our first kinematic quantity we'll need for problem solving. Beyond that, if we call the direction of motion positive, the object will have a positive acceleration (i.e. speeding up) as it falls.

Choosing a Frame of Reference

An important first step in analyzing objects in free fall is deciding what direction along the y-axis we are going to call positive and which direction will therefore be negative. Although you can set your positive direction any way you want and get the correct answer, following the hints below can simplify your work to reach that correct answer:

1. Identify what direction the object will initially move and assign that as your positive direction. In this case the positive y-direction will point toward the bottom of the paper.
2. With the axes identified you can now identify and write down your given information. Of course, you'll need to identify a third given from the problem information in order to solve for your unknowns:
   • v_i=0
   • v_f=?
   • d=?
   • a=9.81 m/s²
   • t=?
3. Notice the direction the vector arrows are drawn drawn -- if the velocity and acceleration point in the same direction, the object speeds up. If they point in opposite directions, the object slows down.

KEY CONCEPT: The magnitude of the acceleration due to gravity (g) is a constant 9.81 m/s² on the surface of Earth. For the purposes of this discussion we will say that as long as an object is in the air near the surface of the Earth, it is always experiencing acceleration with a magnitude of g.

Objects Launched Upward

Examining the motion of an object being launched vertically upward is done in much the same way we examined the motion of an object falling from rest. The major difference is we have to look at two components to its motion instead of one... Up and Down... instead of just down.

Before we get into establishing our frame of reference and working through the quantitative analysis let's build a solid conceptual understanding of what is happening while the ball is in the air. Consider the ball being thrown vertically into the air as shown in the diagram at right.

Question: In order for the ball to move upwards can it's initial velocity be zero?

Answer: No, in order for the object to go up its initial velocity must be greater than zero.

Question: What happens to the velocity as the ball is in the air?

Answer: As the ball rises its velocity decreases until it reaches its maximum height, stops, and begins to fall. As the ball falls, the velocity increases. In other words the ball is accelerating the entire time it is in the air.

Question: What causes the ball's acceleration?

Answer: Gravity! This means that the acceleration of the ball the entire time it is in the air is 9.81m/s² down provided we are on Earth. Notice that the acceleration can be either +9.81m/s² or -9.81m/s². Which sign it carries is entirely dependent on the direction we have labeled as positive.

Question: How can we describe the motion of the ball as it reaches its maximum altitude?

Answer: Typically motion is described in terms of velocity and acceleration. We have already shown the ball's acceleration for the entire time it is in the air is 9.81m/s² down. This acceleration causes the ball's velocity to decrease at a constant rate until it reaches maximum altitude, at which point it turns around and starts to fall. In order to turn around the ball's velocity must pass through zero. Therefore, at maximum altitude the velocity of the ball must be zero.

Question: How does the time to reach maximum altitude compare to the time to fall back down?

Answer: Since gravity provides the same acceleration to the ball on the way up (slowing it down) as on the way down (speeding it up), the time to reach maximum altitude is the same as the time to return to its launch position. In similar fashion, the initial velocity of the ball on the way up will equal the velocity of the ball at the instant it reaches the point from which it was launched on the way down.

Choosing a Frame of Reference

Now that we have established a conceptual understanding of the ball's motion we can begin to establish a quantitative solution. As with any problem, that solution starts with establishing our frame of reference.

Following the rule of thumb established previously, we will assign the direction the ball
begins to move as positive. (Remember that assigning positive and negative directions are completely arbitrary. You have the freedom to assign them how you see fit. Once you assign them, however, don't change them).

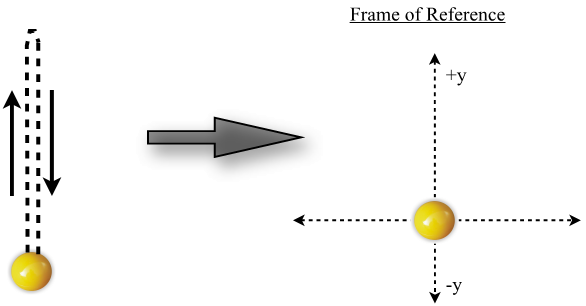
Notice in the figure above we have assigned the up direction as positive. This is simply following the "rule" of assigning the original direction of motion as positive. Remember, now that we've assigned our positive and negative directions we cannot change them. Since we have an object that moves in two different directions (up AND down) it is important that we pay close attention to the vector nature of this object's motion. Let's examine each independently.

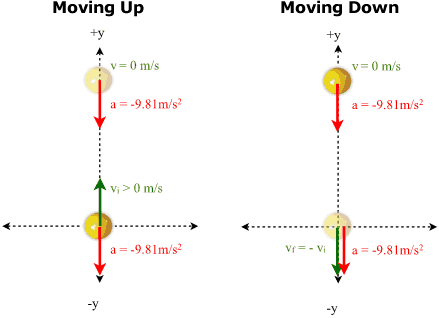
Notice in the "Moving Up" case the acceleration and the velocity are pointing the opposite directions. This means (unsurprisingly) the object will slow down as it travels upward. In the "Moving Down" case, the acceleration vector and the velocity vector point in the same direction. This means the object will speed up as it falls, which is consistent with what we observe every day.

A “trick of the trade” to solving free fall problems in which an object starts moving up, stops, and comes back down involves symmetry.  The time an object takes to reach its highest point is equal to the time it takes to return to the same vertical position.  The speed with which the projectile begins its journey upward is equal to the speed of the projectile when it returns to the same height (although, of course, its velocity is in the opposite direction).  And, if you want to simplify the problem, realize that vertically, at its highest point, for an instant the vertical velocity is 0.  This added information can assist you in filling out your vertical motion tables.  If you cut the object’s motion in half, you can simplify your problem solving – but don’t forget that if you want the total time in the air, you must double the time it takes for the object to rise to its highest point.