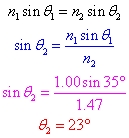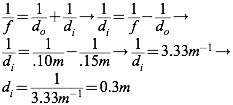Refraction
When a wave reaches the boundary between media, part of the wave is reflected and part of the wave enters the new medium. As the wave enters the new medium, the speed of the wave changes, and the frequency of a wave remains constant, therefore, consistent with the wave equation, v=fλ, the wavelength of the wave must change.
Question: When a wave enters a new material, what happens to its speed, frequency, and wavelength?
Answer: Speed changes, frequency remains constant, and wavelength changes.
The front of a wave has some actual width, therefore if the wave does not impinge upon the boundary between media at a right angle, not all of the wave enters the new medium and changes speed at the same time. This causes the wave to bend as it enters a new medium in a process known as refraction.
To better illustrate this, imagine you're in a line in a marching band, connected with your bandmates as you march at a constant speed down the field in imitation of a wave front. As your wavefront reaches a new medium that slows you down, such as a mud pit, the band members reaching the mud pit slow down before those who reach the pit later. Since you are all connected in a wave front, the entire wave shifts directions (refracts) as it passes through the boundary between field and mud!
The index of refraction (n) is a measure of how much light slows down in a material. In a vacuum, all electromagnetic waves have a speed of c=3*108 m/s. In other materials, light slows down. The ratio of the speed of light in a vacuum to the speed of light in the new material is known as the index of refraction (n). The slower the wave moves in the material, the larger the index of refraction: 
Question: A light ray traveling in air enters a second medium and its speed slows to 1.71 x 108 m/s. What is the absolute index of refraction of the second medium?
Answer:
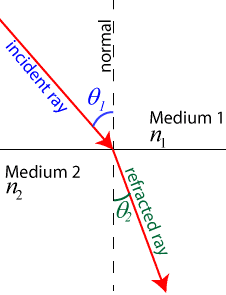
The amount a light wave bends as it enters a new medium is given by the law of refraction, also known as Snell's Law. Snell's Law states that 
, where n1 and n2 are the indices of refraction of the media, and θ corresponds to the angles of the incident and refracted rays, again measured from the normal. Light bends toward the normal as it enters a material with a higher index of refraction (slower material), and bends away from the normal as it enters a material with a lower index of refraction (slower material).
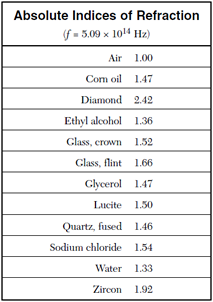
Not only does index of refraction depend upon the medium the light wave is traveling through, it also varies with frequency. Thankfully, its variation is typically fairly small. Table of indices of refraction for common materials at a set frequency is given at right.
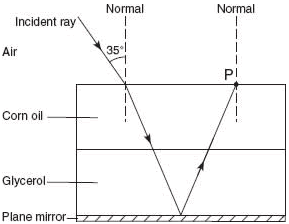
Question: A ray of monochromatic light having a frequency of 5.09 × 1014 hertz is incident on an interface of air and corn oil at an angle of 35° as shown. The ray is transmitted through parallel layers of corn oil and glycerol and is then reflected from the surface of a plane mirror, located below and parallel to the glycerol layer. The ray then emerges from the corn oil back into the air at point P.
Calculate the angle of refraction of the light ray as it enters the corn oil from air.
Answer:
Question: Explain why the ray does not bend at the corn oil-glycerol interface.
Answer: The indices of refraction are the same for corn oil and glycerol (the speed of the wave does not change at the corn-oil / glycerol interface).
Thin Lenses
A common application of refraction is the optical lens. Much like mirrors, lenses come in two types: convex and concave. When working with lenses, however, convex lenses are converging lenses, and concave lenses are diverging lenses.
In the case of lenses, similar rules for ray tracing apply. For a convex lens, a ray parallel to the principal axis is refracted through the far focal point of the lens. In addition, a ray drawn from the object through the center of the lens passes through the center of the lens unbent.
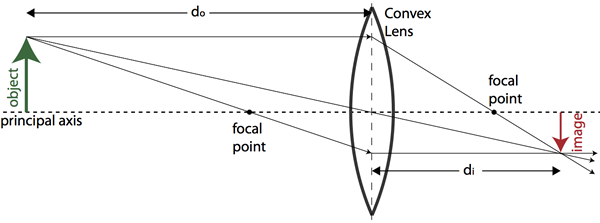
Question: An object is located 0.15 meters from a converging lens with focal length 0.10 meters. How far from the lens is the image formed?
Answer:
Question: A converging lens forms a real image that is four times larger than the object. If the image is located 0.16 meters from the lens, what is the object distance?
Answer: First, realize that since the image is real, the image distance, by convention, is negative. Therefore, you are given the magnification of m=4, and the image distance di=-0.16m. Now you can apply the magnification equation to solve for the object distance do.
For a concave lens, a ray from the object parallel to the principal axis is refracted away from the principal axis on a line from the near focal point through the point where the ray intercepts the center of the lens. In addition, any ray that passes from the object through a focal point is refracted parallel to the principal axis. This leads to upright, virtual, reduced images from concave diverging lenses.
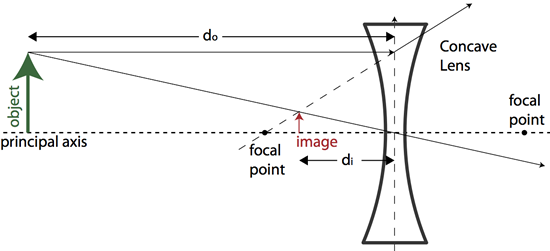
The same equations used for analysis of mirrors also apply to the analysis of thin lenses. Recall the lensmaker’s equation:
Calculation of the magnification of a lens also uses the same equation used in the analysis of mirrors:
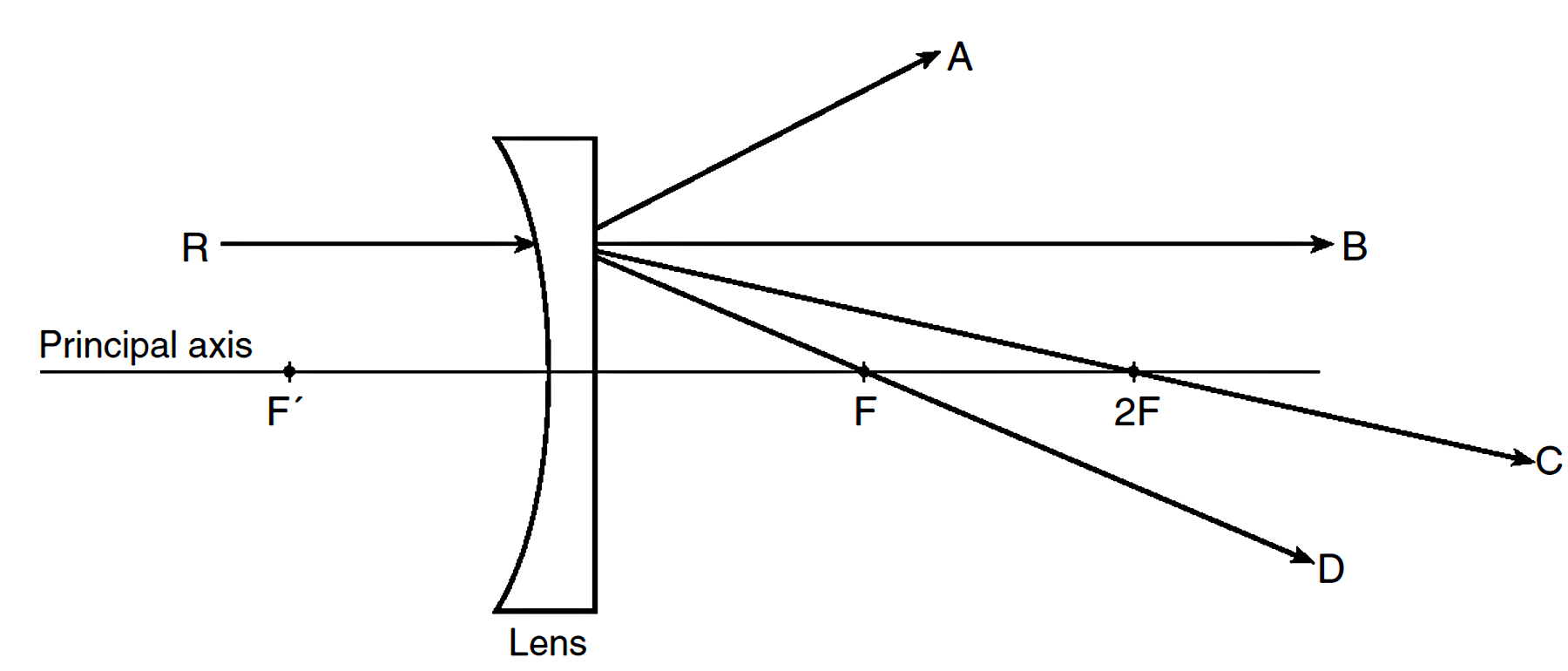
Question: Which ray best represents the path of light ray R after it passes through the lens?
Answer: (A) shows the diverging light ray from a diverging (concave) lens.
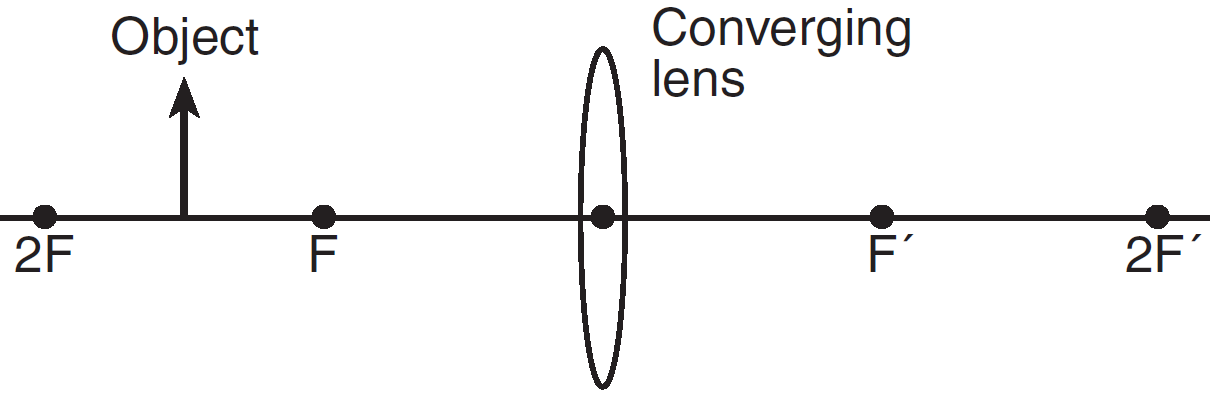
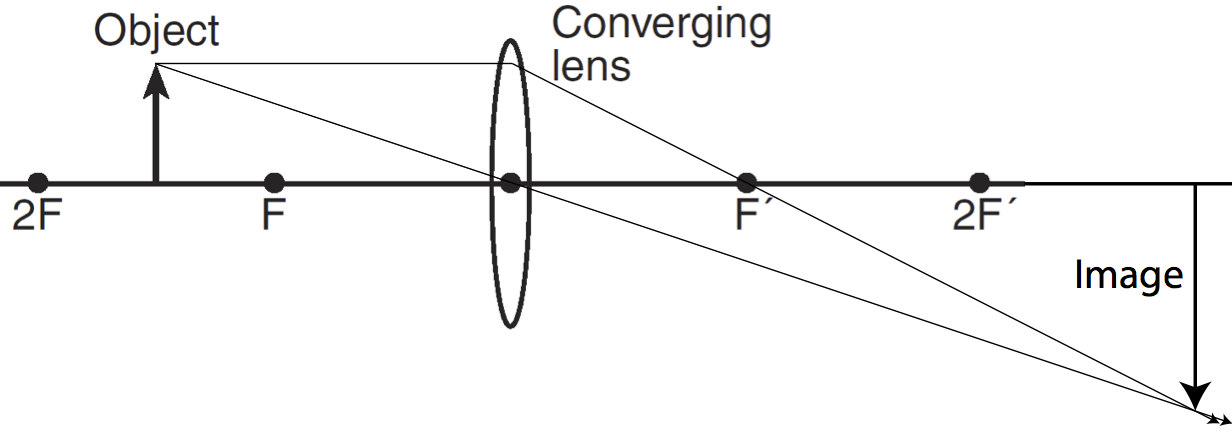
Question: The diagram shows an object placed between 1 and 2 focal lengths from a converging lens. The image of the object produced by the lens is
- real and inverted
- virtual and inverted
- real and erect
- virtual and erect
Answer: (1) real and inverted
