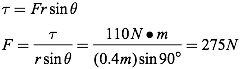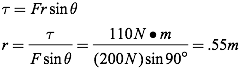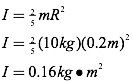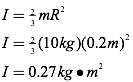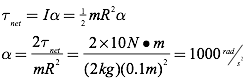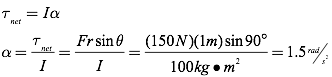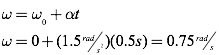Honors Physics - Torque
Torque
Torque (τ) is a force that causes an object to turn. If you think about using a wrench to tighten a bolt, the closer to the bolt you apply the force, the harder it is to turn the wrench, while the farther from the bolt you apply the force, the easier it is to turn the wrench. This is because you generate a larger torque when you apply a force at a greater distance from the axis of rotation.
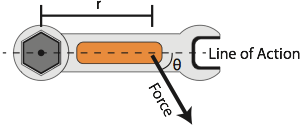
Let’s take a look at the example of a wrench turning a bolt. A force is applied at a distance from the axis of rotation. Call this distance r. When you apply forces at 90 degrees to the imaginary line leading from the axis of rotation to the point where the force is applied (known as the line of action), you obtain maximum torque. As the angle at which the force applied decreases (θ), so does the torque causing the bolt to turn. Therefore, you can calculate the torque applied as:
![]()
In some cases, physicists will refer to the rsinθ as the lever arm, or moment arm, of the system. The lever arm is the perpendicular distance from the axis of rotation to the point where the force is applied. Alternately, you could think of torque as the component of the force perpendicular to the lever multiplied by the distance r. Units of torque are the units of force × distance, or Newton-meters (N·m).

Question: A pirate captain takes the helm and turns the wheel of his ship by applying a force of 20 Newtons to a wheel spoke. If he applies the force at a radius of 0.2 meters from the axis of rotation, at an angle of 80° to the line of action, what torque does he apply to the wheel?
Answer:
Question: A mechanic tightens the lugs on a tire by applying a torque of 110 N·m at an angle of 90° to the line of action. What force is applied if the wrench is 0.4 meters long?
Answer:
Question: How long must the wrench be if the mechanic is only capable of applying a force of 200N?
Answer:
Objects which have no rotational acceleration, or a net torque of zero, are said be in rotational equilibrium. This implies that any net positive (counter-clockwise) torque is balanced by an equal net negative (clockwise) torque.
Moment of Inertia
Previously, the inertial mass of an object (its translational inertia) was defined as that object’s ability to resist a linear acceleration. Similarly, an object’s rotational inertia, or moment of inertia, describes an object’s resistance to a rotational acceleration. The symbol for an object’s moment of inertia is I.
Objects that have most of their mass near their axis of rotation have a small rotational inertia, while objects that have more mass farther from the axis of rotation have larger rotational inertias.
For common objects, you can look up the formula for their moment of inertia. For more complex objects, the moment of inertia can be calculated by taking the sum of all the individual particles of mass making up the object multiplied by the square of their radius from the axis of rotation. This can be quite cumbersome using algebra, and is therefore typically left to calculus-based courses or numerical approximation using computing systems.
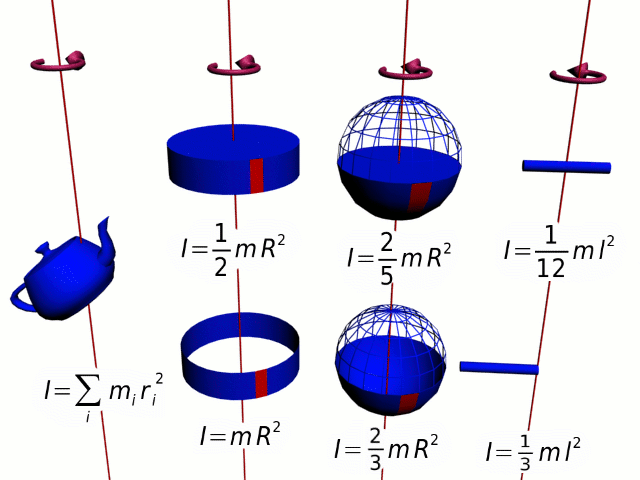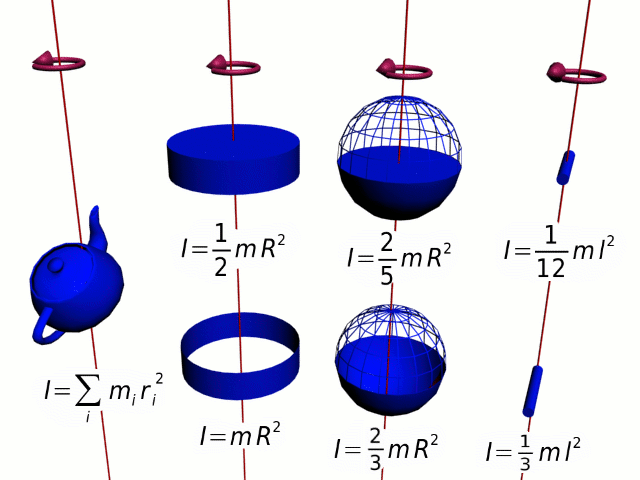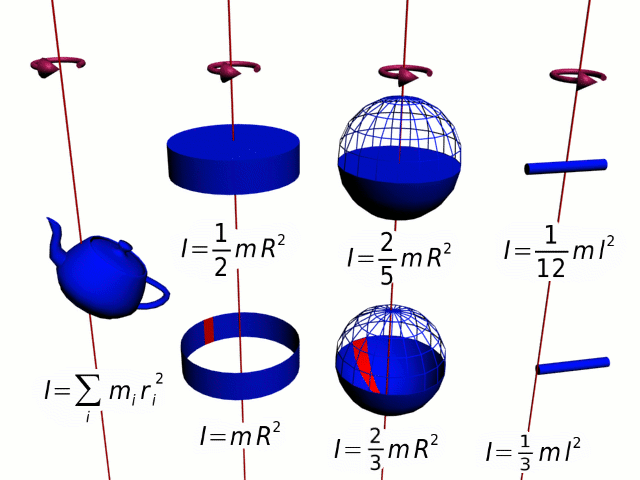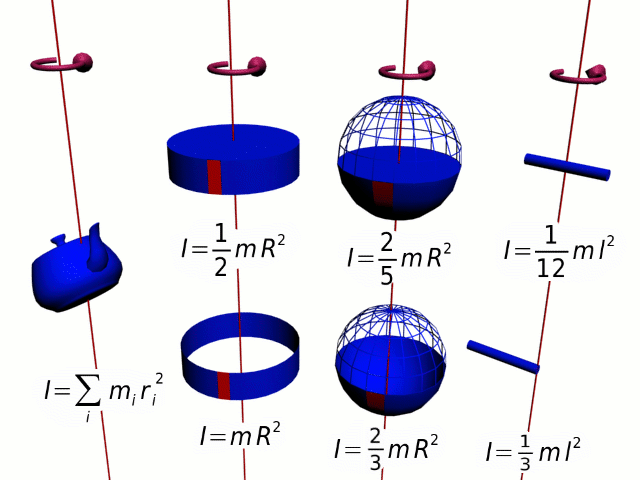
Question: Calculate the moment of inertia for a solid sphere with a mass of 10 kg and a radius of 0.2 m.
Answer:
Question: Calculate the moment of inertia for a hollow sphere with a mass of 10 kg and a radius of 0.2 m.
Answer:
Newton's 2nd Law for Rotation
In the chapter on dynamics, you learned about forces causing objects to accelerate. The larger the net force, the greater the linear (or translational) acceleration, and the larger the mass of the object, the smaller the translational acceleration.
The rotational equivalent of this law, Newton’s 2nd Law for Rotation, relates the torque on an object to its resulting angular acceleration. The larger the net torque, the greater the rotational acceleration, and the larger the rotational inertia, the smaller the rotational acceleration:
Question: What is the angular acceleration experienced by a uniform solid disc of mass 2 kg and radius 0.1 m when a net torque of 10 N·m is applied? Assume the disc spins about its center.
Answer:
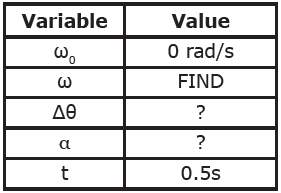
Question: A Round-A-Bout on a playground with a moment of inertia of 100 kg·m2 starts at rest and is accelerated by a force of 150N at a radius of 1m from its center. If this force is applied at an angle of 90° from the line of action for a time of 0.5 seconds, what is the final rotational velocity of the Round-A-Bout?
Answer: Start by making our rotational kinematics table:
Since you only know two items on the table, you must find a third before you solve this with the rotational kinematic equations. Since you are given the moment of inertia of the Round-A-Bout as well as the applied force, you can solve for the angular acceleration using Newton’s 2nd Law for Rotational Motion.
Now, use your rotational kinematics to solve for the final angular velocity of the Round-A-Bout.