The Wave Equation
The frequency (f) of a wave describes the number of waves that pass a given point in a time period of one second. The higher the frequency, the more waves that pass. Frequency is measured in number of waves per second (1/s), also known as a Hertz (Hz). If 60 waves pass a given point in a second, the frequency of the wave would be 60 Hz.
Closely related to frequency, the period (T) of a wave describes how long it takes for a single wave to pass a given point, and can be found as the reciprocal of the frequency. Period is a measurement of time, and therefore is measured in seconds. Both frequency and period were introduced earlier in our discussion of circular motion.
Question: What is the period of a 60-hertz electromagnetic wave traveling at 3.0×108 meters per second?
Answer:
Because waves move through space, they must have a velocity. The velocity of a wave is a function of the type of wave, and the medium it travels through. Electromagnetic waves moving through a vacuum, for instance, travel at roughly 3*108 m/s. This value is so famous and common in physics it is given its own symbol, c. When an electromagnetic wave enters a different medium, such as glass, it slows down. If the same wave were to then re-emerge from glass back into a vacuum, it would again travel at c, or 3*108 m/s.
The speed of a wave can be easily related to its frequency and wavelength. Speed of a wave is determined by the wave type and the medium its traveling through. For a given wave speed, as frequency increases, wavelength must decrease, and vice versa. This can be shown mathematically using the wave equation: ![]() .
.
Question: In a vacuum, all electromagnetic waves have the same:
- speed
- phase
- frequency
- wavelength
Answer: (1) speed.
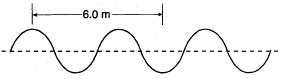
Question: The diagram below represents a periodic wave traveling through a uniform medium. If the frequency of the wave is 2.0 hertz, find the speed of the wave.
Answer: The diagram shows a length of 6m for 1.5 wavelengths, therefore the wavelength (λ) must be 4m. Given both wavelength and frequency, we can use the wave equation to find the wave speed: