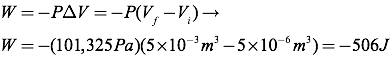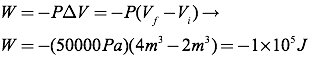Thermodynamics
Thermodynamics, which began as an effort to increase the efficiency of steam engines in the early 1800s, can be thought of as the study of the relationship between heat transferred to or from an object, and the work done on or by an object. Both heat and work deal with the transfer of energy, but heat in- volves energy transfer due to a temperature difference.
The zeroth law of thermodynamics (don’t blame me, I didn’t name it!) states that if object A is in thermal equilibrium with object B, and object B is in thermal equilibrium with object C, then objects A and C must be in thermal equilibrium with each other. This law is so intuitive it almost doesn’t need stating, but in defining proofs of the 1st and 2nd laws of thermodynamics, scientists realized they needed this law specifically stated to complete their proofs.
The first law of thermodynamics is really a restatement of the law of conservation of energy. Specifically, it states that the change in the internal energy of a closed system is equal to the heat added to the system plus the work done on the system, and is written as:
In this equation it is important to note the sign conventions, where a positive value for heat, Q, represents heat added to the system, and a positive value for work, W, indicates work done on the gas. If energy were being pulled from the system, as in heat taken from the system or work done by the system, those quantities would be negative.
In most cases, you’ll utilize the first law of thermodynamics to analyze the behavior of ideal gases, which can be streamlined by analyzing the definition of work on a gas.
If work is force multiplied by displacement, and pressure is force over area, force can be replaced with pressure multiplied by area. The area multiplied by the displacement gives you the change in volume of the gas. Due to the sign convention that work done on the gas is positive (corresponding to a decrease in volume), you can write work as W=-PΔV.
Question: Five thousand joules of heat is added to a closed system, which then does 3000 joules of work. What is the net change in the internal energy of the system?
Answer:
Question: A liquid is changed to a gas at atmospheric pressure (101,325 Pa). The volume of the liquid was 5×10-6 m3. The volume of gas is 5×10-3 m3. How much work was done in the process?
Answer:
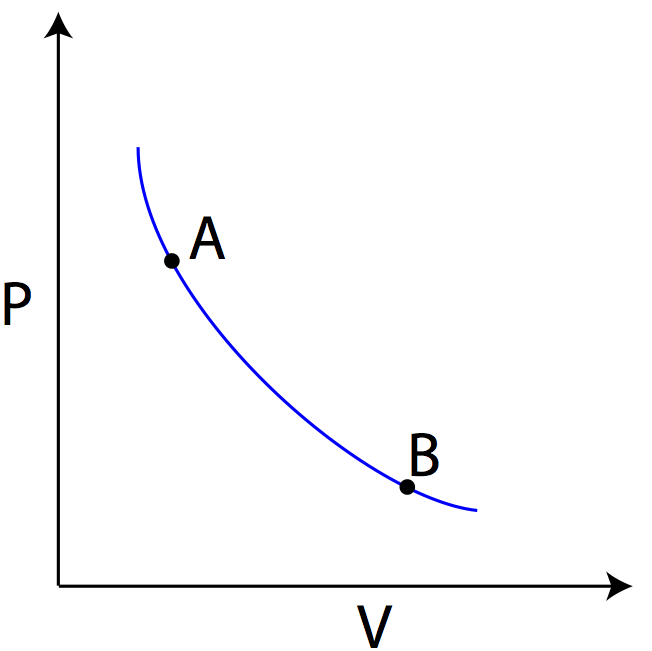
Pressure-Volume Diagrams (PV diagrams) are useful tools for visualizing the thermodynamic processes of gases. These diagrams show pressure on the y-axis, and volume on the x-axis, and are used to describe the changes undergone by a set amount of gas. Because the amount of gas remains constant, a PV diagram not only tells you pressure and volume, but can also be used to determine the temperature of a gas when combined with the ideal gas law. A Sample PV diagram is shown below, showing two states of the gas, state A and state B.
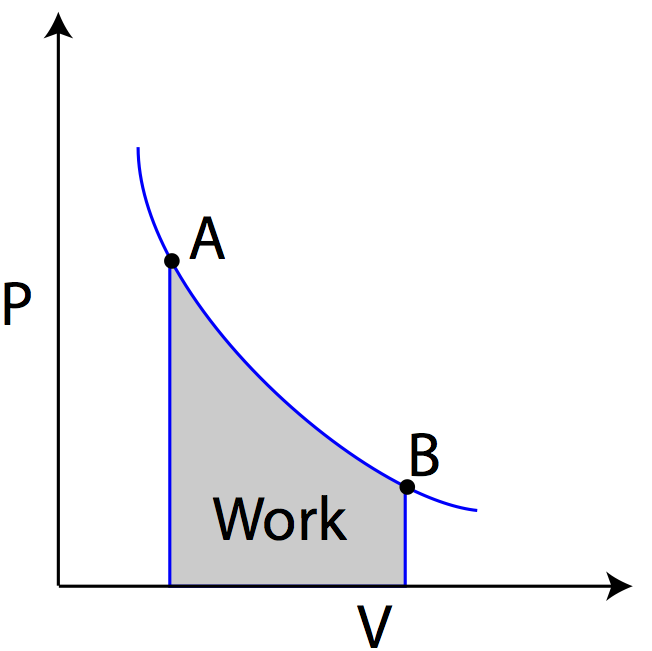
In transitioning from state A to state B, the volume of the gas increases, while the pressure of the gas decreases. In transitioning from state B to state A, the volume of the gas decreases, while the pressure increases. Because the work done on the gas is given by W=-PΔV, you can find the work done on the gas graphically from the PV diagram by taking the area under the curve. Because of the positive/negative sign convention, as the volume of gas expands the gas does work (W is negative), and as the gas compresses, work is done on the gas (W is positive).
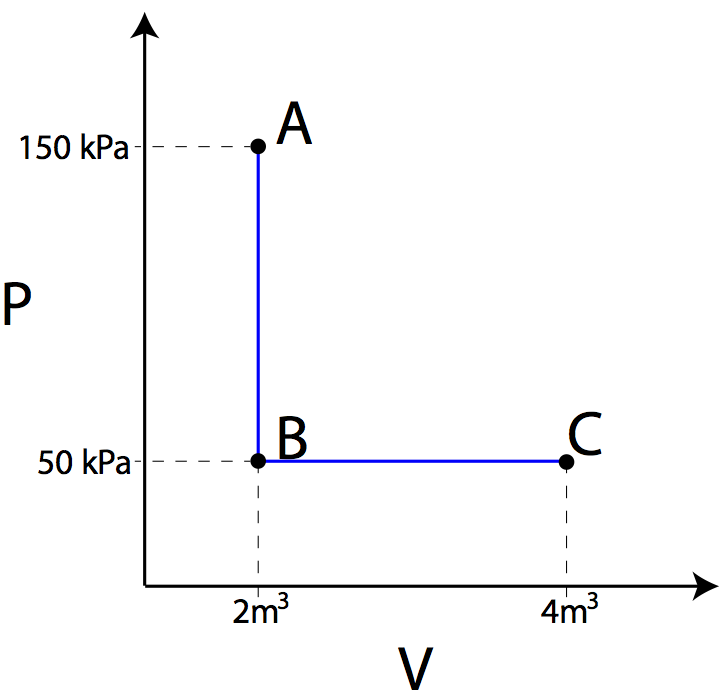
Question: Using the PV diagram at right, find the amount of work required to transition from state A to B, and then the amount of work required to transition from state B to state C.
Answer: The amount of work in moving from state A to B is equal to the area under the graph for that transition. Since there is no area under the straight line, no work was done. The work in moving from state B to state C can be found by taking the area under the line in the PV diagram.
Note that the work is negative, indicating the gas did work, which correlates with the gas expanding.
In exploring ideal gas state changes, there are a number of state changes in which one of the characteristics of the gas or process remain constant, and are illustrated on the PV diagram below.
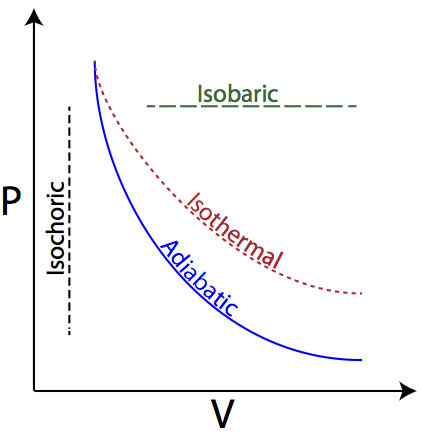
The types of processes include:
- Adiabatic -- Heat (Q) isn’t transferred into or out of the system
- Isobaric -- Pressure (P) remains constant
- Isochoric -- Volume (V) remains constant
- Isothermal -- Temperature (T) remains constant
In an adiabatic process, heat flow (Q) is zero. Applying the first law of thermodynamics, if ΔU=Q+W, and Q is 0, the change in internal energy of the gas must be equal to the work done on the gas (ΔU=W).
In an isobaric process, pressure of the gas remains constant. Because pressure is constant, the PV diagram for an isobaric process shows a horizontal line. Further, applying this to the ideal gas law, you find that V/T must remain constant for the process.
In an isochoric process, the volume of the gas remains constant. The PV diagram for an isochoric process is a vertical line. Because W=-PΔV, and ΔV=0, the work done on the gas is zero. This is also reflected graphically in the PV diagram. Work can be found by taking the area under the PV graph, but the area under a vertical line is zero. Applying this to the ideal gas law, you find that P/T must remain constant for an isochoric process.
In an isothermal process, temperature of the gas remains constant. Lines on a PV diagram describing any process held at constant temperature are therefore called isotherms. In an isothermal process, the product of the pressure and the volume of the gas remains constant. Further, because temperature is constant, the internal energy of the gas must remain constant.
Question: An ideal gas undergoes an adiabatic expansion, doing 2000 joules of work. How much does the gas’s internal energy change?
Answer: Since the process is adiabatic, Q=0, therefore:
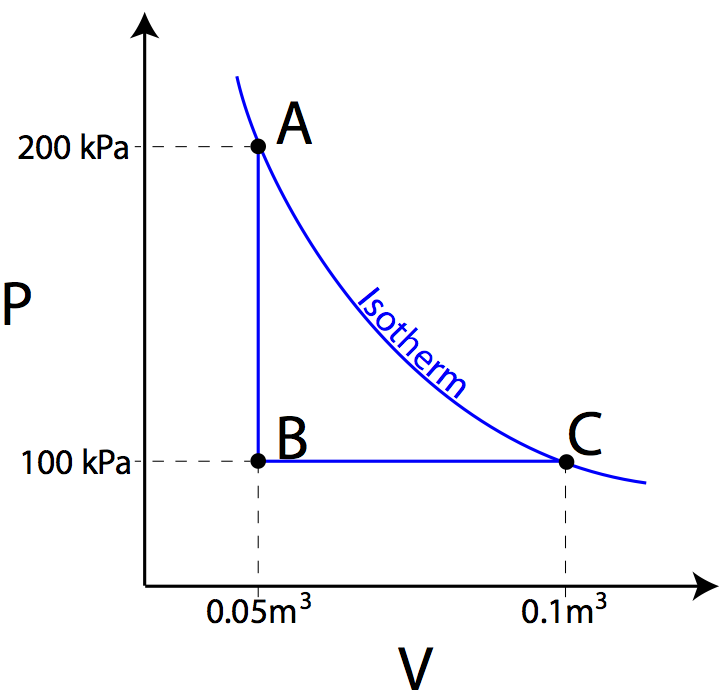
Question: Heat is removed from an ideal gas as its pressure drops from 200 kPa to 100 kPa. The gas then expands from a volume of 0.05 m3 to 0.1 m3 as shown in the PV diagram below. If curve AC represents an isotherm, find the work done by the gas and the heat added to the gas.
Answer: The work done by the gas in moving from A to B is zero, as the area under the graph is zero. In moving from B to C, however, the work done by the gas can be found by taking the area under the graph.
The negative sign indicates that 5000 joules of work was done by the gas. Since AC is on an isotherm, the temperature of the gas must remain constant, therefore the gas’s internal energy must remain constant. Knowing that ΔU=Q+W, if ΔU=0, then Q must be equal to -W, therefore 5000 joules must have been added to the gas.
The second law of thermodynamics can be stated in a variety of ways. One statement of this law says that heat flows naturally from a warmer object to a colder object, and cannot flow from a colder object to a warmer object without doing work on the system. This can be observed quite easily in everyday circumstances. For example, your cold spoon contacting your hot soup never results in your soup becoming hotter and your spoon becoming colder.
The second law of thermodynamics also limits the efficiency of any heat engine, and proves that it is not possible to make a 100 percent efficient heat engine, even if friction were completely eliminated.
Another statement of this law says that the level of entropy, or disorder, in a closed system can only increase or remain the same. This means that your desk will never naturally become more organized without doing work. It also means that you can’t drop a handful of plastic building blocks and observe them spontaneously land in an impressive model of a medieval castle. Unfortunately, it even means that no matter how many times Humpty Dumpty falls off his wall, all his pieces on the ground will never end up more organized after he hits the ground compared to before his balance failed him.
The final law of thermodynamics, the third law of thermodynamics, also known as Nernst’s Theorem after its discoverer, Walter Nernst, states that no material can ever be cooled to absolute zero (although materials can get awfully close!)
