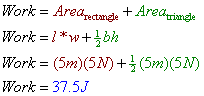Work

Defining Work

Sometimes we work hard. Sometimes we're slackers. But, right now, are you doing work? And what do we mean by work?

Work -- the process of moving an object by applying a force

In order for a force to qualify as having done work on an object, there must be a displacement and the force must cause the displacement.

I'm sure you can think up countless examples of work being done, but a few that spring to my mind include pushing a snowblower to clear the driveway, pulling a sled up a hill with a rope, stacking boxes of books from the floor onto a shelf, and throwing a baseball from the pitcher's mound to home plate.

Let's try an exercise: Which of the following are examples of work being done?

1. Sandy struggles to push her stalled car, but can't make it move.
2. Jeeves the butler carries a tray above his head by one arm across the room at a constant velocity.
3. A missile streaks through the upper atmosphere.

Each of these examples help us better understand the definition of work. In example 1, even though Sandy pushes her car, with all her might, the car doesn't move, therefore no work is done.

Example 2 is a very tricky situation. In this scenario, Jeeves applies a force upward with his arm, but the tray moves horizontally. From this perspective, the force of the butler's arm isn't causing the displacement, therefore you could say no work is done by his arm. However, Jeeves' legs are pushing him forward, and therefore the tray moves horizontally, so you could say from this perspective he is doing work on the tray. (In actuality, the situation is even more complex than this as we pull friction and normal forces into the equation, but for the sake of clarity, let's move on...)

In example 3, the missile's engines are applying a force causing it to move. But what is doing the work? The hot expanding gas is pushed backward out of the missile's engine... so, using Newton's 3rd Law, we observe the reactionary force of the gas pushing the missile forward, causing a displacement. Therefore, the expanding exhausted gas is doing work on the missile!

Calculating Work

Mathematically, work can be expressed by the following equation:

Where W is the work done, F is the force applied, in Newtons, and d is the object's displacement, in meters.

The units of work can be found by a unit analysis of the work formula. If work is force multiplied by distance, the units must be the units of force multiplied by the units of distance, or newtons multiplied by meters. A newton-meter is also known as a Joule (J).

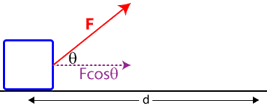
It's important to note that when using this equation, only the force applied in the direction of the object's displacement counts! This means that if the force and displacement vectors aren't in exactly the same direction, you need to take the component of force in the direction of the object's displacement. To do this, line up the force and displacement vectors tail-to-tail and measure the angle between them. Since this component of force can be calculated by multiplying the force times the cosine of the angle between the force and displacement vectors, we can re-write our work equation as:

Let's examine a few more examples:

Question: An appliance salesman pushes a refrigerator 2 meters across the floor by applying a force of 200N. Find the work done.

Answer: Since the force and displacement are in the same direction, the angle between them is 0: .

Question: A friend's car is stuck on the ice. You push down on the car to provide more friction for the tires (by way of increasing the normal force), allowing the car's tires to propel it forward 5m onto less slippery ground. How much work did you do?

Answer: You applied a downward force, yet the car's displacement was sideways. Therefore, the angle between the force and displacement vectors is 90°, so: .

Question: You push a crate up a ramp with a force of 10N. Despite your pushing, however, the crate slides down the ramp a distance of 4m. How much work did you do?

Answer: Since the direction of the force you applied is opposite the direction of the crate's displacement, the angle between the two vectors is 180°.

Question: How much work is done in lifting an 8-kg box from the floor to a height of 2m above the floor?

Answer: It's easy to see the displacement is 2m, and the force must be applied in the direction of the displacement, but what is the force? To lift the box we must match and overcome the force of gravity on the box. Therefore, the force we must apply is equal to the gravitational force, or weight, of the box:

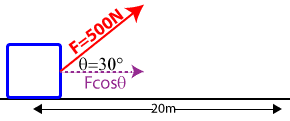
Question:Barry, John, and Sidney pull a 30-kg wagon with a force of 500N a distance of 20m. The force acts at a 30° angle to the horizontal. Calculate the work done.

Answer:

Force vs. Displacement Graphs

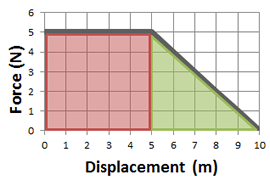
The area under a force vs. displacement graph is the work done by the force. Consider the situation of a block being pulled across a table with a constant force of 5 Newtons over a displacement of 5 meters, then the force gradually tapers off over the next 5 meters.

The work done by the force moving the block can be calculated by taking the area under the force vs. displacement graph (a combination of a rectangle and triangle) as follows: