Waves and Sound

Defining & Describing Waves

A pulse is a single disturbance which carries energy through a medium or through space. Imagine you and your friend holding opposite ends of a slinky. If you quickly move your arm up and down, a single pulse will travel down the slinky toward your friend.

If, instead, you generate several pulses at regular time intervals, you now have a wave carrying energy down the slinky. A wave, therefore is a repeated disturbance which carries energy. The mass of the slinky doesn't move from end of the slinky to the other, but the energy it carries does.

When a pulse or wave reaches a hard boundary, it reflects off the boundary, and is inverted. If a pulse or wave reaches a soft, or flexible, boundary, it still reflects off the boundary, but does not invert.

Waves can be classified in several different waves. One type of wave, known as a mechanical wave, requires a medium (or material) through which to travel. Examples of mechanical waves include water waves, sound waves, slinky waves, and even seismic waves. Electromagnetic waves, on the other hand, do not require a medium in order to travel. Electromagnetic waves (or EM waves) are considered part of the Electromagnetic Spectrum. Examples of EM waves include light, radio waves, microwaves, and even X-rays.

Further, waves can be classified based upon their direction of vibration. Waves in which the "particles" of the wave vibrate in the same direction as the wave direction are known as longitudinal, or compressional, waves. Examples of longitudinal waves include sound waves and seismic P waves. Waves in which the particles of the wave vibrate perpendicular to the wave's direction of motion are known as transverse waves. Examples of transverse waves include seismic S waves, electromagnetic waves, and even stadium waves (the "human" waves you see at a baseball or football game!).

 

 

 

 

 

 

 

 

 

 

Wave Anatomy

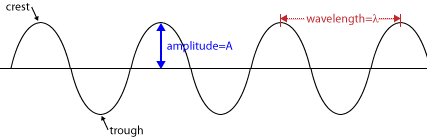
Waves have a number of characterisics which define their behavior. Looking at a transverse wave, we can identify specific locations on the wave. The highest points on the wave are known as crests. The lowest points on the wave are known as troughs. The amplitude of the wave, corresponding to the energy of the wave, is the distance from the baseline to a crest or the baseline to a trough.

The length of the wave, or wavelength, noted with the Greek letter lambda (λ), is the distance between corresponding points on consecutive waves (i.e. crest to crest or trough to trough). Points on the same wave with the same displacement from equilibrium moving in the same direction (such as a crest to a crest or a trough to a trough) are said to be in phase (phase difference is 0° or 360°). Points with opposite displacements from equilibrium (such as a crest to a trough) are said to be 180° out of phase.

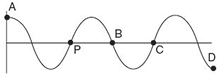
Question: The diagram represents a periodic wave. Which point on the wave is in phase with point P?

Answer: Point C is in phase with point P, since point C represents a point with the same displacement from equilibrium moving in the same direction. Points that are in phase are located one or more whole wavelengths apart on a wave.

 

Question: Two waves having the same frequency and amplitude are traveling in the same medium. Maximum constructive interference occurs at points where the phase difference between the two superposed waves is:

Answer: 0°.

 

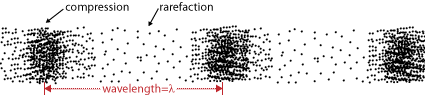
In similar fashion, longitudinal, or compressional, waves also have amplitude and wavelength. In the case of longitudinal waves, however, instead of crests and troughs, the longitudinal waves have areas of high density (compressions) and areas of low density (rarefactions), as shown in the representation of the particles of a sound wave. The wavelength, then, of a compressional wave is the distance between compressions, or the distance between rarefactions. Once again, the amplitude corresponds to the energy of the wave.

Question: A longitudinal wave moves to the right through a uniform medium, as shown below. Points A, B, C, D, and E represent the positions of particles of the medium. What is the direction of the motion of the particles at position C as the wave moves to the right?

Answer: The particles move to the left and right at position C, as the particles in a longitudinal wave vibrate parallel to the wave velocity:

Question: Between which two points on the wave could you measure a complete wavelength?

Answer: You could measure a complete wavelength between points A and C, since A and C represent the same point on successive waves.