Digital Logic
Now that you know how a single transistor functions, how can you put transistors together to make a computer? In order to answer that question, you must start with a brief introduction to digital logic.
Begin with the examination of a single FET. In order to simplify the analysis, you can assume that zero voltage refers to a logic state of false, represented by a zero, and a negative voltage strong enough to turn the gate on refers to a logic state of 1, or true. The ouput of the device is given by current flow, where a zero represents no current flow (state=false), and a one represents current flow (state=true). The source is connected to zero bias and served as a reference.
| G | D | Current Flow |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
As the table shows, the output of the FET, the current flow, is false unless both the gate and the drain are true. This type of analysis can be extended to more complex configurations of transistors.
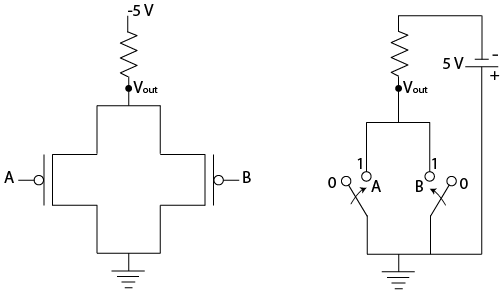
Question: Build the truth table for the two-transistor structure shown below. Note that the ground symbol at the bottom of the schematic indicates zero voltage. A corresponding switch representation is shown to the right of the transistor schematic.
Answer: Building the truth table, you find that Vout is only true when both A and B are false.
A B Vout 0 0 1 0 1 0 1 0 0 1 1 0
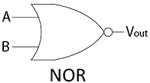
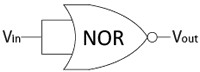
This is known as a NOR (NOT OR) gate, and can be represented with the simpler digital logic schematic shown.
Question: Build the truth table for the two-transistor structure shown below.
Answer: Building the truth table, you find that Vout is only true when both A and B are true.
A B Vout 0 0 0 0 1 0 1 0 0 1 1 1
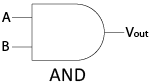
This is known as an AND gate, and can be represented with the simpler digital logic schematic shown.
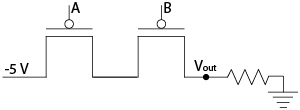
Question: Build the truth table for the following configuration of a NOR gate where the two inputs are tied together.
Answer: Building the truth table, you find that Vout gives the opposite state of Vin.
Vin Vout 0 1 1 0
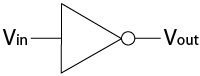
By tying the inputs of a NOR gate together, you have created what is known as an inverter... whatever state goes in, the opposite state goes out. An inverter can be represented on a schematic diagram with the symbol shown below.
As you are beginning to see, using just these simple switches you can build more and more complex devices. But what about something more practical? How do you go from inverter, NOR, and AND gates to a computer?
You continue to build more and more complex devices from these fundamental parts in incremental fashion. To provide a practical example, a half-adder is a device that performs very basic binary addition. It takes two binary inputs A and B (with values of either 0 or 1), and outputs the Sum of those of values, as shown in the following truth table. Note that if both inputs are a 1, the output, a binary two (1 0), includes not just a sum output, but also a Carry output to be "carried over" to the next mathematical operation.
| A | B | Sum | Carry |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
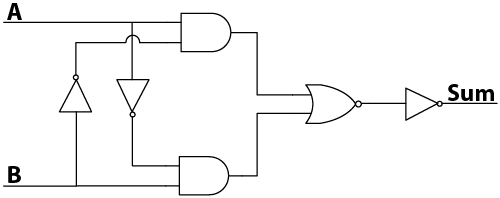
Creating the logic for the "Sum" output can be done in a variety of ways using a variety of gates. One combination using both inverter, AND, and NOR gates is shown below. See if you can verify the truth table above by walking through the logic functions using the device below.
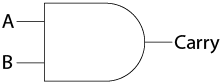
The logic for the Carry output is considerably simpler. Careful observation of the required output state given the input states indicates that the Carry can be made with a single AND gate.
Digital clocks, calculators, microwaves, radios, televisions, and computers are all run by integrated circuits consisting of hundreds, thousands, millions, and even billions of transistors connected in various configurations to execute a wide range of increasingly complex logic functions.
How, then, do you put millions and billions of these transistors onto a tiny piece of silicon the size of a fingernail? To answer that question, you must enter the realm of microelectronic fabrication!