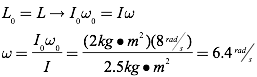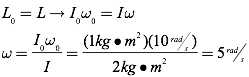Honors Physics - Angular Momentum
Previously, you learned that linear momentum, the product of an object’s mass and its velocity, is conserved in a closed system. In similar fashion, spin angular momentum L, the product of an object’s moment of inertia and its angular velocity about the center of mass, is also conserved in a closed system with no external net torques applied.

This can be observed by watching a spinning ice skater. As an ice skater launches into a spin, she generates rotational velocity by applying a torque to her body. The skater now has an angular momentum as she spins around an axis which is equal to the product of her moment of inertia (rotational inertia) and her rotational velocity.
To increase the rotational velocity of her spin, she pulls her arms in close to her body, reducing her moment of inertia. Angular momentum is conserved, therefore rotational velocity must increase. Then, before coming out of the spin, the skater reduces her rotational velocity by move her arms away from her body, increasing her moment of inertia.
Question: Angelina spins on a rotating pedestal with an angular velocity of 8 radians per second. Bob throws her an exercise ball, which increases her moment of inertia from 2 kg·m2sup> to 2.5 kg·m2. What is Angelina’s angular velocity after catching the exercise ball? (Neglect any external torque from the ball.)
Answer: Since there are no external torques, you know that the initial spin angular momentum must equal the final spin angular momentum, and can therefore solve for Angelina’s final angular velocity:
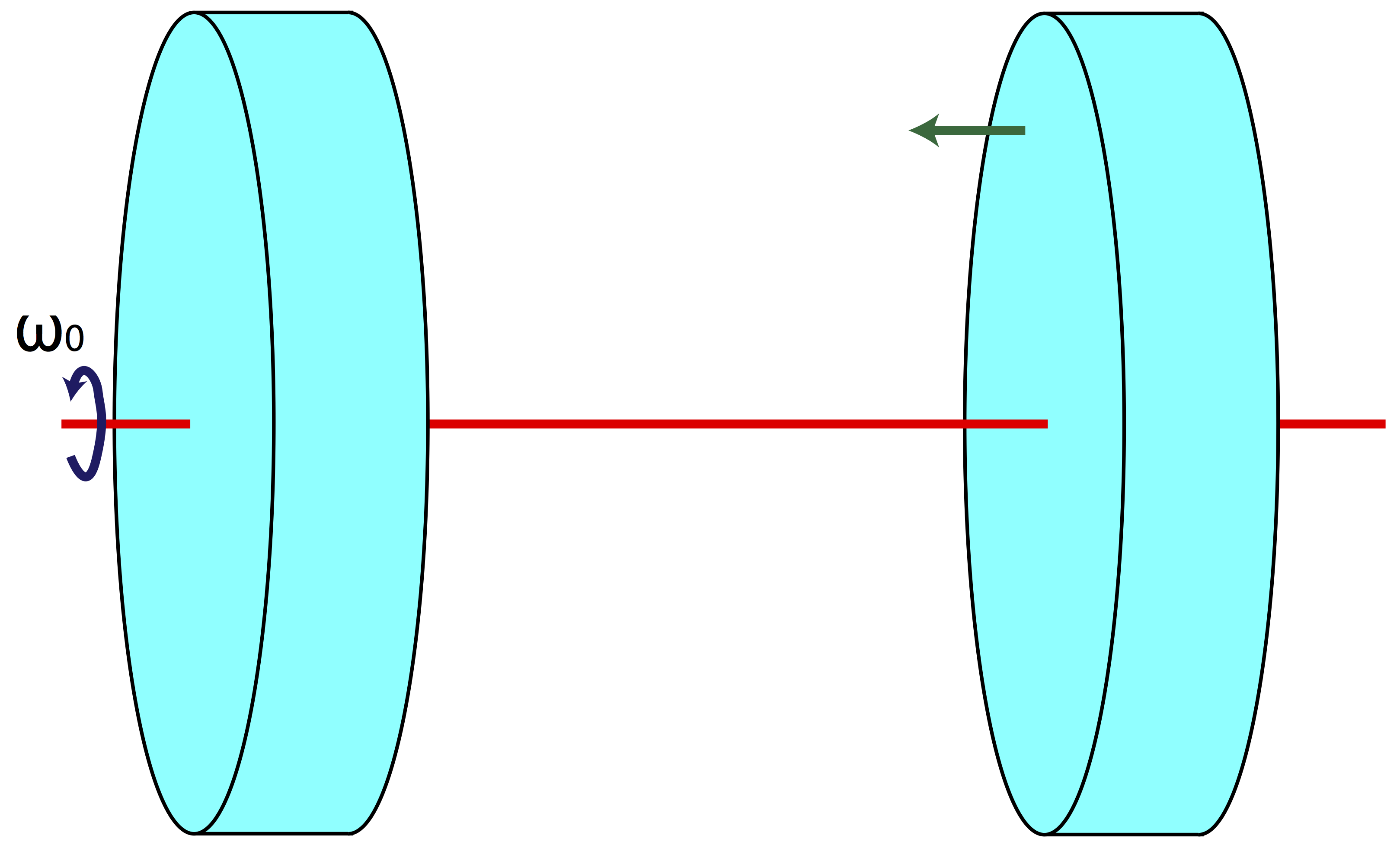
Question: A disc with moment of inertia 1 kg·m2 spins about an axle through its center of mass with angular velocity 10 rad/s. An identical disc which is not rotating is slid along the axle until it makes contact with the first disc. If the two discs stick together, what is their combined angular velocity?
Answer: Once again, since there are no external torques, you know that spin angular momentum must be conserved. When the two discs stick together, their new combined moment of inertia must be the sum of their individual moments of inertia, for a total moment of inertia of 2 kg·m2.