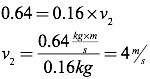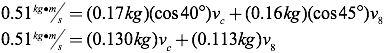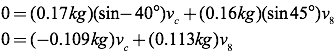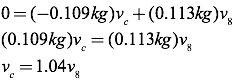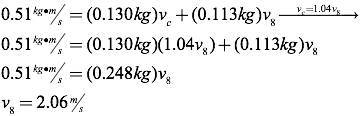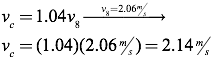Types of Collisions

When objects collide, a number of different things can happen depending on the characteristics of the colliding objects. Of course, you know that momentum is always conserved in a closed system. Imagine, though, the differences in a collision if the two objects colliding are super-bouncy balls compared to two lumps of clay. In the first case, the balls would bounce off each other. In the second, they would stick together and become, in essence, one object. Obviously, you need more ways to characterize collisions.

Elastic collisions occur when the colliding objects bounce off of each other. This typically occurs when you have colliding objects which are very hard or bouncy. Officially, an elastic collision is one in which the sum of the kinetic energy of all the colliding objects before the event is equal to the sum of the kinetic energy of all the objects after the event. Put more simply, kinetic energy is conserved in an elastic collisions.

NOTE: There is no law of conservation of kinetic energy -- IF kinetic energy is conserved in a collision, it is called an elastic collision, but there is no physical law that requires this.

Inelastic collisions occur when two objects collide and kinetic energy is not conserved. In this type of collision some of the initial kinetic energy is converted into other types of energy (heat, sound, etc.), which is why kinetic energy is NOT conserved in an inelastic collision. In a perfectly inelastic collision, the two objects colliding stick together.

In reality, most collisions fall somewhere between the extremes of a completely elastic collision and a completely inelastic collision.

 

Question: Two billiard balls collide. Ball 1 moves with a velocity of 4 m/s, and ball 2 is at rest. After the collision, ball 1 comes to a complete stop. What is the velocity of ball 2 after the collision? Is this collision elastic or inelastic? The mass of each ball is 0.16 kg.

Answer: To find the velocity of ball 2, use a momentum table.

Objects	Momentum Before (kg×m/s)	Momentum After (kg×m/s)
Ball 1	0.16×4=.64	0
Ball 2	0	0.16×v2
Total	0.64	0.16×v2

To determine whether this is an elastic or inelastic collision, you can calculate the total kinetic energy of the system both before and after the collision.

Objects	KE Before (J)	KE After (J)
Ball 1	0.50×0.16×42=1.28	0
Ball 2	0	0.50×0.16×42=1.28
Total	1.28	1.28

 

Since the kinetic energy before the collision is equal to the kinetic energy after the collision (kinetic energy is conserved), this is an elastic collision.

 

Collisions in Two Dimensions

Much like the key to projectile motion, or two-dimensional kinematics problems, was breaking up vectors into their x- and y-components, the key to solving two-dimensional collision problems involves breaking up momentum vectors into x- and y- components. The law of conservation of momentum then states that momentum is independently conserved in both the x- and y- directions.

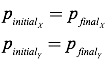
Therefore, you can solve two-dimensional collision problems by creating a separate momentum table for the x-component of momentum before and after the collision, and a momentum table for the y-component of momentum.

 

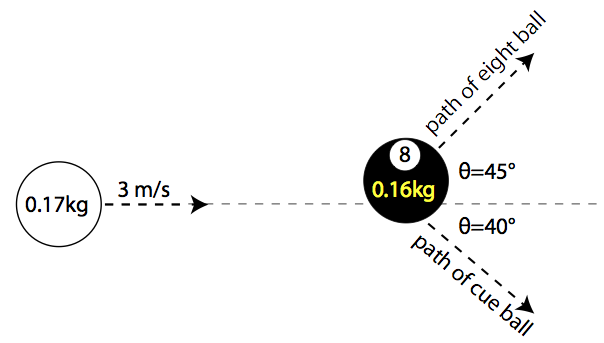
Question: Bert strikes a cue ball of mass 0.17 kg, giving it a velocity of 3 m/s in the x-direction. When the cue ball strikes the eight ball (mass=0.16 kg), previously at rest, the eight ball is deflected 45 degrees from the cue ball’s previous path, and the cue ball is deflected 40 degrees in the opposite direction. Find the velocity of the cue ball and the eight ball after the collision.

Answer: Start by making momentum tables for the collision, beginning with the x-direction. Since you don’t know the velocity of the balls after the collision, call the velocity of the cue ball after the collision v_c, and the velocity of the eight ball after the collision v₈. Note that you must use trigonometry to determine the x-component of the momentum of each ball after the collision.

Objects	X Momentum Before (kg×m/s)	X Momentum After (kg×m/s)
Cue Ball	0.17×3=0.51	0.17×vc×cos(40°)
Eight Ball	0	0.16×v8×cos(45°)
Total	0.51	0.17×vc×cos(40°)+ 0.16×v8×cos(45°)

Since the total momentum in the x-direction before the collision must equal the total momentum in the x-direction after the collision, you can set the total before and total after columns equal:

Next, create a momentum table and algebraic equation for the conservation of momentum in the y-direction.

Objects	Y Momentum Before (kg×m/s)	Y Momentum After (kg×m/s)
Cue Ball	0	0.17×vc×sin(-40°)
Eight Ball	0	0.16×v8×sin(45°)
Total	0	0.17×vc×sin(-40°)+ 0.16×v8×sin(45°)

You now have two equations with two unknowns. To solve this system of equations, start by solving the y-momentum equation for v_c.

You can now take this equation for v_c and substitute it into the equation for conservation of momentum in the x-direction, effectively eliminating one of the unknowns, and giving a single equation with a single unknown.

Finally, solve for the velocity of the cue ball after the collision by substituting the known value for v₈ into the result of the y-momentum equation.