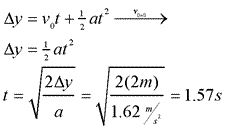Honors Physics - Kinematic Equations
Developing the Toolset
Motion graphs such as the position-time, velocity-time, and acceleration-time graphs are terrific tools for understanding motion. However, there are times when graphing motion may not be the most efficient or effective way of understanding the motion of an object. To assist in these situations, you can add a set of problem-solving equations to your physics toolbox, known as the kinematic equations. These equations can help you solve for key variables describing the motion of an object when you have a constant acceleration. Once you know the value of any three variables, you can use the kinematic equations to solve for the other two!
| Variable | Meaning |
|---|---|
| v0 | Initial velocity |
| v | Final velocity |
| Δx | Displacement |
| a | Acceleration |
| t | Time elapsed |
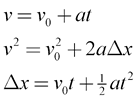
Problem Solving Strategy
In using these equations to solve motion problems, it’s important to take care in setting up your analysis before diving in to a solution. Key steps to solving kinematics problems include:
- Labeling your analysis for horizontal (x-axis) or vertical (y-axis) motion.
- Choosing and indicating a positive direction (typically the direction of initial motion).
- Creating a motion analysis table (v0, v, Δx, a, t). Note that Δx is a change in position, or displacement, and can be re-written as x-x0.
- Using what you know about the problem to fill in your “givens” in the table.
- Once you know three items in the table, use kinematic equations to solve for any unknowns.
- Verify that your solution makes sense.
Take a look at a sample problem to see how this strategy can be employed.
Sample Problems
These equations and problem solving steps are applicable to both horizontal and vertical motion problems. Let’s try them out:
This problem solving strategy and the kinematic equations work for vertical motion problems as well:
In some cases, you may not be able to solve directly for the "find" quantity. In these cases, you can solve for the other unknown variable first, then choose an equation to give you your final answer:

Question: An astronaut drops a hammer from 2.0 meters above the surface of the Moon. If the acceleration due to gravity on the Moon is 1.62 meters per second2, how long will it take for the hammer to fall to the Moon’s surface?
Answer: