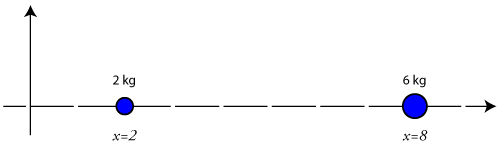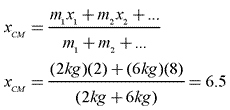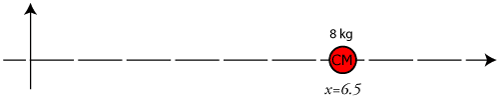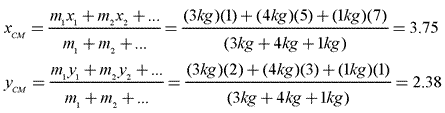Honors Physics - Center of Mass
Defining Center of Mass
The motion of real objects is considerably more complex than that of simple theoretical particles. However, we can treat an entire object as if its entire mass were contained at a single point, known as the object's center of mass (CM). Mathematically, the center of mass of an object is the weighted average of the location of mass in an object.
We can find the center of mass of a system of particles by taking the sum of the mass of the particles, multiplied by their positions, and dividing that by the total mass of the object. Looking at this in two dimensions, the center of mass in the x- and y-directions would be:
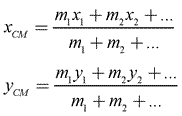
No matter how complex an object may be, we can calculate its center of mass and then treat the object as a point particle with total mass M. This allows us to apply our basic physics principles to complex objects without adding unnecessary mathematical complexity to our analyses!
Center of Mass in 1-D
Sample Problem: Find the center of mass of an object modeled as two separate masses on the x-axis. The first mass is 2 kg at an x-coordinate of 2 and the second mass is 6 kg at an x-coordinate of 8.
Answer:
Center of Mass in Multiple Dimensions
We can use the same strategy for finding the center of mass of a multi-dimensional object.
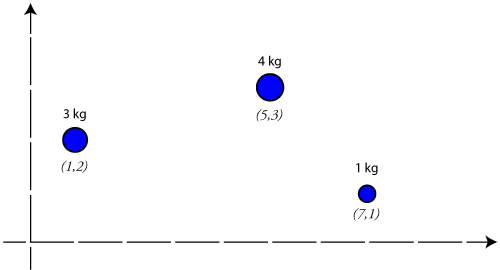
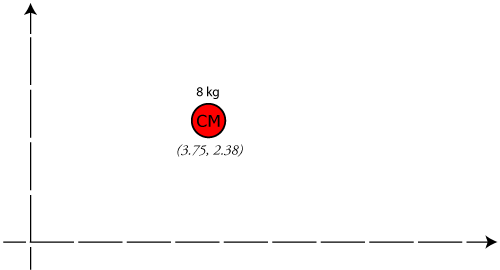
Sample Problem: Find the coordinates of the center of mass for the system shown below.
Answer:
Center of Gravity
Note that center of mass is not the same as center of gravity. In a uniform gravitational field, they are the same, but center of gravity refers to the location at which the force of gravity acts upon an object as if it were a point particle with all its mass focused at that point, a subtle but important difference.